Question

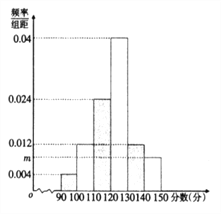
【题目】某学校为了解高三复习效果，从高三第一学期期中考试成绩中随机抽取50名考生的数学成绩，分成6组制成频率分布直方图如图所示：

（1）求的值及这50名同学数学成绩的平均数；

（2）该学校为制定下阶段的复习计划，从成绩在的同学中选出3位作为代表进行座谈，若已知成在的同学中男女比例为2：1，求至少有一名女生参加座谈的概率.

Answer 1

【答案】(1) ，121.8(2)

【解析】试题分析：（1）先根据频率分布直方图中小长方形面积等于对应区间的概率，所以小长方形面积和为1，因此求得m;根据组中值与对应区间概率乘积的和等于平均值得；（2）先根据比例得男生4人，女生2人，再利用枚举法得从6名同学中选出3人的所有事件数，确定其中不含女生的事件数，得至少有一名女生事件数，最后根据古典概型概率公式求概率

试题解析：（Ⅰ）由题 解得

（Ⅱ）由频率分布直方图可知，成绩在的同学有（人），

由比例可知男生4人，女生2人，记男生分别为A、B、C、D；女生分别为x、y，

则从6名同学中选出3人的所有可能如下：ABC、ABD、ABx、ABy、ACD、ACx、ACy、ADx、ADy、BCD、BCx、BCy、BDx、BDy、CDx、CDy、Axy、Bxy、Cxy、Dxy——共20种

其中不含女生的有4种ABC、ABD、ACD、BCD

设：至少有一名女生参加座谈为事件A

则