Question

【题目】如图，正方形与梯形所在的平面互相垂直，，，，，为的中点.

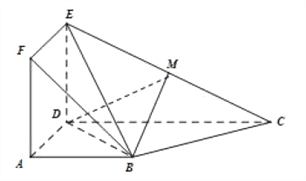
（1）求证：平面；

（2）求证：平面平面；

（3）求平面与平面所成锐二面角的余弦值.

Answer 1

【答案】（1）证明过程详见解析；（2）证明过程详见解析；（3）.

【解析】

试题本题主要考查中位线、平行四边形的证明、线面平行、线面垂直、面面垂直、二面角等基础知识，考查学生的空间想象能力、逻辑推理能力、计算能力.第一问，作出辅助线MN，N为中点，在中，利用中位线得到，且，结合已知条件，可证出四边形ABMN为平行四边形，所以，利用线面平行的判定，得∥平面；第二问，利用面面垂直的性质，判断面，再利用已知的边长，可证出，则利用线面垂直的判定得平面BDE，再利用面面垂直的判定得平面平面；第三问，可以利用传统几何法证明二面角的平面角，也可以利用向量法建立空间直角坐标系，求出平面BEC和平面ADEF的法向量，利用夹角公式计算即可.

（1）证明：取中点，连结．

在△中，

分别为的中点，所以∥，且

．由已知∥，，所以

∥，且．所以四边形为平行四边形，

所以∥．

又因为平面，且平面，

所以∥平面．

（2）证明：在正方形中，．又因为

平面平面，且平面平面，

所以平面．所以．

在直角梯形中，，，可得．

在△中，，所以．

所以平面．

又因为平面，所以平面平面．

（3）（方法一）延长和交于．

在平面内过作于,连结．由平面平面，

∥，，平面平面=，

得，于是．

又，平面，所以，

于是就是平面与平面所成锐二面角的

平面角.

由，得.

又，于是有.

在中，.

所以平面与平面所成锐二面角的余弦值为．

（方法二）由（2）知平面，且．

以为原点，所在直线分别为轴，建立空间直角坐标系．

易得.平面的一个法向量为.设为平面的一个法向量，因为，所以，令，得．

所以为平面的一个法向量．

设平面与平面所成锐二面角为．

则．所以平面与平面所成锐二面角的余弦值为．