Question

【题目】已知函数，.

（1）当时，求函数的单调递增区间；

（2）对于，为任意实数，关于的方程恰好有两个不等实根，求实数的值；

（3）在（2）的条件下，若不等式在恒成立，求实数的取值范围.

Answer 1

【答案】（1），；（2）；（3）.

【解析】

（1）利用和与差公式化简，结合正弦函数的图象及性质即可求解函数的单调递增区间；

（2）根据，，求解内层函数的范围，结合恰好有两个不等实根，即可求解实数的值；（3）根据（2）中的值；可得解析式，，上，求解的值域，不等式成立，即可求解实数的取值范围．

(1)

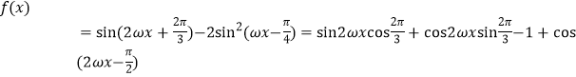
（1）当时，可得函数

令，

得

函数的单调递增区间为，，．

（2）当，时，，其周期

关于的方程恰好有两个不等实根，即恰好有两个不等实根，

可得；

（3）根据（2）中；可得

，，

，，

那么的值域为，

不等式成立，

即

此时