题目内容
【题目】设向量
，
，令函数
，若函数
的部分图象如图所示，且点
的坐标为
.
（1）求点
的坐标；
（2）求函数的单调增区间及对称轴方程；
（3）若把方程
的正实根从小到大依次排列为
，求
的值.
【答案】(1) 
(2) 单调递增区间为
；对称轴方程为
，
；(3)14800
【解析】
（1）先求出
，令
求出点B的坐标；（2）利用复合函数的单调性原理求函数
的单调增区间，利用三角函数的图像和性质求对称轴方程；（3）由（2）知对称轴方程为，，所以
，
，…，
，即得解.
解:（1）
由已知
，得
∴
令，得
，，∴
，.
当时，
，∴
得坐标为
（2）单调递增区间
，得
，
∴单调递增区间为
对称轴
，得，
∴对称轴方程为，
（3）由
，得
，
根据正弦函数图象的对称性，且由（2）知对称轴方程为，
∴，，…，
∴
练习册系列答案
王后雄学案教材完全解读系列答案
相关题目
【题目】某工厂新研发了一种产品，该产品每件成本为5元，将该产品按事先拟定的价格进行销售，得到如下数据：
单价 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量 | 90 | 84 | 83 | 80 | 75 | 68 |
（1）求销量
（件）关于单价
（元）的线性回归方程
；
（2）若单价定为10元，估计销量为多少件；
（3）根据销量关于单价的线性回归方程，要使利润
最大，应将价格定为多少？
参考公式：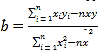
，
.参考数据：
，
【题目】小王每天自己开车上班，他在路上所用的时间
（分钟）与道路的拥堵情况有关.小王在一年中随机记录了200次上班在路上所用的时间，其频数统计如下表，用频率近似代替概率.
| 15 | 20 | 25 | 30 |
频数（次） | 50 | 50 | 60 | 40 |
（Ⅰ）求小王上班在路上所用时间的数学期望
；
（Ⅱ）若小王一周上班5天，每天的道路拥堵情况彼此独立，设一周内上班在路上所用时间不超过的天数为
，求的分布列及数学期望.
