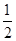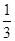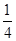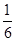题目内容
数列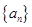 的前n项和记为Sn,a1=t,点(Sn,an+1)在直线y=2x+1上,n∈N*.
的前n项和记为Sn,a1=t,点(Sn,an+1)在直线y=2x+1上,n∈N*.
(1)当实数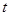 为何值时,数列
为何值时,数列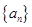 是等比数列?
是等比数列?
(2)在(1)的结论下,设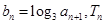 是数列
是数列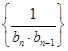 的前
的前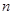 项和,求
项和,求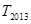 的值.
的值.
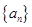 的前n项和记为Sn,a1=t,点(Sn,an+1)在直线y=2x+1上,n∈N*.
的前n项和记为Sn,a1=t,点(Sn,an+1)在直线y=2x+1上,n∈N*.(1)当实数
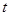 为何值时,数列
为何值时,数列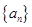 是等比数列?
是等比数列?(2)在(1)的结论下,设
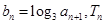 是数列
是数列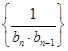 的前
的前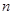 项和,求
项和,求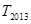 的值.
的值.(1)当实数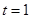 时,数列
时,数列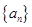 是等比数列;(2)
是等比数列;(2)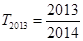 .
.
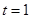 时,数列
时,数列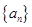 是等比数列;(2)
是等比数列;(2)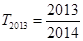 .
.试题分析:(1)首先由已知得
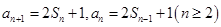 ,两式相减得
,两式相减得 ,整理得
,整理得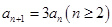 ,要使数列
,要使数列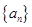 是等比数列,必须且只需
是等比数列,必须且只需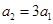 ,由此列出关于
,由此列出关于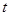 的方程
的方程 ,解此方程,即可求得实数
,解此方程,即可求得实数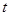 的值(也可以利用
的值(也可以利用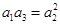 列出关于
列出关于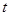 的方程求解);(2) 由(1)得知
的方程求解);(2) 由(1)得知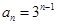 ,
,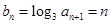 ,进而得
,进而得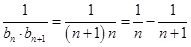 ,根据此式的结构特征,最后利用裂项相消法,即可求得
,根据此式的结构特征,最后利用裂项相消法,即可求得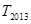 的值.
的值.试题解析:(1)解:由题意得
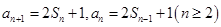 ,
,两式相减得
 ,即
,即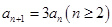 , 4分
, 4分所以当
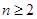 时,
时,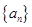 是等比数列.要使
是等比数列.要使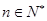 时,
时,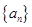 是等比数列,则只需
是等比数列,则只需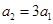 ,
,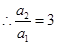 ,
,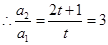 ,从而
,从而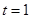 . 7分
. 7分(可以利用
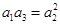 可酌情给分)
可酌情给分)(2)由(1)得知
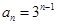 ,
,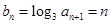 , 9分
, 9分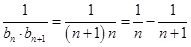 , 12分
, 12分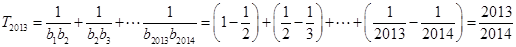 . 14分.
. 14分. 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
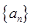 的前
的前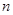 项和为
项和为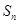 ,
,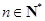 ,且
,且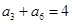 ,
,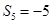 .
.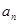 ;
;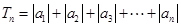 ,求
,求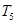 的值和
的值和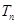 的表达式.
的表达式.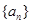 是公比大于1的等比数列,
是公比大于1的等比数列,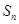 为其前
为其前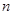 项和已知
项和已知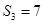 ,且
,且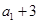 ,
,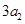 ,
,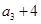 构成等差数列.
构成等差数列.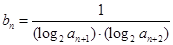 ,求数列
,求数列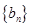 的前
的前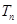 .
.
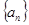 和
和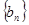 的前
的前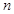 项和分别为
项和分别为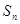 和
和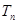 ,且
,且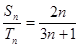 ,则
,则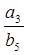 =( )
=( )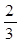
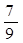
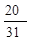
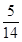
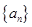 中,
中,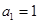 ,
,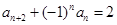 ,记
,记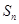 是数列
是数列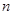 项和,则
项和,则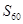 = .
= . 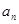 }的前n项和为
}的前n项和为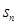 ,若
,若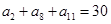 ,那么
,那么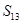 = .
= .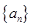 中,
中,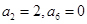 且数列
且数列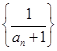 是等差数列,则
是等差数列,则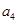 =( )
=( )