题目内容
设直线x+ky-1=0被圆O:x2+y2=2所截弦的中点的轨迹为M,则曲线M与直线x-y-1=0位置关系为( )
| A.相离 | B.相切 | C.相交 | D.不确定 |
如图,直线x+ky-1=0恒过定点A(1,0),
由平面几何知识得,OM⊥AM,
从而中点M的轨迹是以OA为直径的圆,
其方程为:(x-
)2+y2=
,
由圆的方程得到圆心坐标(
,0),半径r=
,
则圆心(
,0)到直线x-y-1=0的距离d=
<r=
,
所以直线与圆的位置关系是相交.
故选C.
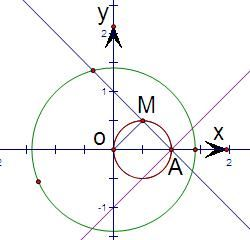
由平面几何知识得,OM⊥AM,
从而中点M的轨迹是以OA为直径的圆,
其方程为:(x-
| 1 |
| 2 |
| 1 |
| 4 |
由圆的方程得到圆心坐标(
| 1 |
| 2 |
| 1 |
| 2 |
则圆心(
| 1 |
| 2 |
| 1 | ||
2
|
| 1 |
| 2 |
所以直线与圆的位置关系是相交.
故选C.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目