题目内容
设直线y=ax+b与双曲线3x2-y2=1交于A、B,且以AB为直径的圆过原点,求点P(a,b)的轨迹方程.
由
,
消去y得:(a2-3)x2+2abx+b2+1=0.
∵直线与双曲线交于A、B两点,
∴
,解得a2<3.
设A(x1,y1),B(x2,y2),
可得x1+x2=
,x1•x2=
.
∴y1•y2=(ax1+b)(ax2+b)=a2x1x2+ab(x1+x2)+b2,
又∵以AB为直径的圆过原点,
∴
⊥
,得x1x2+y1y2=0,
由此可得x1x2+[a2x1x2+ab(x1+x2)+b2]=0,
即(1+a2)x1x2+ab(x1+x2)+b2=0,
可得:(1+a2)•
-ab•
+b2=0,化简得:a2-2b2=-1.
因此,点P(a,b)的轨迹方程为x2-2y2=-1,即2y2-x2=1(x2<3).
|
消去y得:(a2-3)x2+2abx+b2+1=0.
∵直线与双曲线交于A、B两点,
∴
|
设A(x1,y1),B(x2,y2),
可得x1+x2=
| 2ab |
| 3-a2 |
| b2+1 |
| a2-3 |
∴y1•y2=(ax1+b)(ax2+b)=a2x1x2+ab(x1+x2)+b2,
又∵以AB为直径的圆过原点,
∴
| OA |
| OB |
由此可得x1x2+[a2x1x2+ab(x1+x2)+b2]=0,
即(1+a2)x1x2+ab(x1+x2)+b2=0,
可得:(1+a2)•
| b2+1 |
| a2-3 |
| 2ab |
| 3-a2 |
因此,点P(a,b)的轨迹方程为x2-2y2=-1,即2y2-x2=1(x2<3).

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
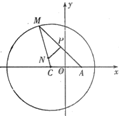
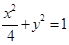 的弦
的弦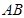 的中点为
的中点为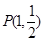 ,则弦
,则弦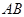 所在直线的方程是 .
所在直线的方程是 .