题目内容
【题目】经销商经销某种农产品,在一个销售季度内,每售出![]() 该产品获利润500元,未售出的产品,每
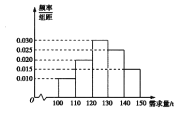
该产品获利润500元,未售出的产品,每![]() 亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了
亏损300元.根据历史资料,得到销售季度内市场需求量的频率分布直方图,如图所示.经销商为下一个销售季度购进了![]() 该农产品.以
该农产品.以![]() (单位:
(单位: ![]() )表示下一个销售季度内的市场需求量,
)表示下一个销售季度内的市场需求量, ![]() (单位:元)表示下一个销售季度内经销该农产品的利润.
(单位:元)表示下一个销售季度内经销该农产品的利润.
(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)根据直方图估计利润![]() 不少于57000元的概率;
不少于57000元的概率;
(3)在直方图的需求量分组中,以各组的区间中点值代表该组的各个值,并以需求量落入该区间的频率作为需求量取该区间中点值的概率(例如:若需求量![]() ,则取
,则取![]() ,且
,且![]() 的概率等于需求量落入
的概率等于需求量落入![]() 的频率),求
的频率),求![]() 的数学期望.
的数学期望.
【答案】(1)![]() (2)0.7.
(2)0.7.
(3)![]() 的分布列为
的分布列为
![]()
![]() .
.
【解析】试题分析:(1)根据题意分段求函数解析式,利用利润等于获利与亏损之和列函数关系式(2)先根据函数解析式求出利润![]() 不少于57000元对应自变量范围,再根据频率分布直方图确定自变量对应区间概率(3)先根据组中值得随机变量,再根据频率分布直方图确定对应概率,最后根据数学期望公式求期望
不少于57000元对应自变量范围,再根据频率分布直方图确定自变量对应区间概率(3)先根据组中值得随机变量,再根据频率分布直方图确定对应概率,最后根据数学期望公式求期望
试题解析:(1)当![]() 时,
时, ![]() ,
,
当![]() 时,
时, ![]() .
.
所以![]()
(2)由(1)知利润![]() 不少于57000元当且仅当
不少于57000元当且仅当![]() .
.
由直方图知需求量![]() 的频率为0.7,所以下一个销售季度内的利润
的频率为0.7,所以下一个销售季度内的利润![]() 不少于57000元的概率的估计值为0.7.
不少于57000元的概率的估计值为0.7.
(3)依题意可得![]() 的分布列为
的分布列为
![]()
所以![]() .
.

练习册系列答案
相关题目
