题目内容
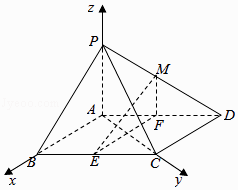
【题目】如图,在四棱锥P﹣ABCD中,底面ABCD是平行四边形,∠BCD=135°,侧面PAB⊥底面ABCD,∠BAP=90°,AB=AC=PA=2,E,F分别为BC,AD的中点,点M在线段PD上. 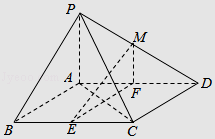
(Ⅰ)求证:EF⊥平面PAC;
(Ⅱ)如果直线ME与平面PBC所成的角和直线ME与平面ABCD所成的角相等,求 ![]() 的值.
的值.
【答案】(Ⅰ)证明:∵在平行四边形ABCD中,∠BCD=135°,∴∠ABC=45°, ∵AB=AC,∴AB⊥AC.
∵E,F分别为BC,AD的中点,∴EF∥AB,
∴EF⊥AC.
∵侧面PAB⊥底面ABCD,且∠BAP=90°,
∴PA⊥底面ABCD.
又EF底面ABCD,
∴PA⊥EF.
又∵PA∩AC=A,PA平面PAC,AC平面PAC,
∴EF⊥平面PAC.
(Ⅱ)解:∵PA⊥底面ABCD,AB⊥AC,∴AP,AB,AC两两垂直,
以A为原点,分别以AB,AC,AP为x轴、y轴和z轴建立空间直角坐标系如图:
则A(0,0,0),B(2,0,0),C(0,2,0),P(0,0,2),D(﹣2,2,0),E(1,1,0),
∴ ![]() =(2,0,﹣2),
=(2,0,﹣2), ![]() =(﹣2,2,﹣2),
=(﹣2,2,﹣2), ![]() ,
, ![]() =(1,1,﹣2).
=(1,1,﹣2).
设 ![]() =λ(0≤λ≤1),则
=λ(0≤λ≤1),则 ![]() =(﹣2λ,2λ,﹣2λ),
=(﹣2λ,2λ,﹣2λ),
∴ ![]() =
= ![]() =(1+2λ,1﹣2λ,2λ﹣2),
=(1+2λ,1﹣2λ,2λ﹣2),
显然平面ABCD的一个法向量为 ![]() =(0,0,1).
=(0,0,1).
设平面PBC的法向量为 ![]() =(x,y,z),
=(x,y,z),
则 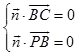 ,即
,即 ![]()
令x=1,得 ![]() =(1,1,1).
=(1,1,1).
∴cos< ![]() ,
, ![]() >=
>= 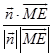 =
= 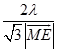 ,cos<
,cos< ![]() >=
>= 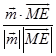 =
= ![]() .
.
∵直线ME与平面PBC所成的角和此直线与平面ABCD所成的角相等,
∴| 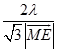 |=|
|=| ![]() |,即
|,即 ![]() ,
,
解得 ![]() ,或
,或 ![]() (舍).
(舍).
∴ ![]() .
.
【解析】(I)由平行四边形的性质可得AB⊥AC,即EF⊥AC,由面面垂直的性质得出PA⊥平面ABCD,故PA⊥EF,故EF⊥平面PAC;(II)以A为原点建立空间直角坐标系,设 ![]() =λ(0≤λ≤1),求出平面PBC,平面ABCD的法向量
=λ(0≤λ≤1),求出平面PBC,平面ABCD的法向量 ![]() 及
及 ![]() 的坐标,根据线面角相等列方程解出λ.
的坐标,根据线面角相等列方程解出λ.

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案【题目】某县共有户籍人口60万人,该县60岁以上、百岁以下的人口占比13.8%,百岁及以上的老人15人.现从该县60岁及以上、百岁以下的老人中随机抽取230人,得到如下频数分布表:
年龄段(岁) | [60,70) | [70,80) | [80,90) | [90,99) |
人数(人) | 125 | 75 | 25 | 5 |
(1)从样本中70岁及以上老人中采用分层抽样的方法抽取21人进一步了解他们的生活状况,则80岁及以上老人应抽多少人?
(2)从(1)中所抽取的80岁及以上的老人中,再随机抽取2人,求抽到90岁及以上老人的概率;
(3)该县按省委办公厅、省人民政府办公厅《关于加强新时期老年人优待服务工作的意见》精神,制定如下老年人生活补贴措施,由省、市、县三级财政分级拨款. ①本县户籍60岁及以上居民,按城乡居民养老保险实施办法每月领取55元基本养老金;
②本县户籍80岁及以上老年人额外享受高龄老人生活补贴.
(a)百岁及以上老年人,每人每月发放345元生活补贴;
(b)90岁及以上、百岁以下老年人,每人每月发放200元的生活补贴;
(c)80岁及以上、90岁以下老年人,每人每月发放100元的生活补贴.
试估计政府执行此项补贴措施的年度预算.
