题目内容
二次函数y=ax2+bx+c(x∈R)的部分对应值如表:
则不等式cx2+bx+a≥0的解集为 .
| -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | |
| 10 | 4 | 0 | -2 | -2 | 0 | 4 | 10 |
考点:一元二次不等式的解法
专题:函数的性质及应用,不等式的解法及应用
分析:根据表中数据得出函数y=ax2+bx+c(x∈R)的两个零点值,由此求出a、b、c的关系,化简不等式cx2+bx+a≥0,求出解集来.
解答:
解:根据表中数据得,二次函数y=ax2+bx+c(x∈R)的两个零点是-2和1,且a>0,
∴方程ax2+bx+c=0的两个实数根是-2和1;
由根与系数的关系得,
;
∴c<0,且c=-2a,b=a;
∴不等式cx2+bx+a≥0可化为2x2-x-1≤0,
解得-
≤x≤1;
∴该不等式的解集为[-
,1].
故答案为:[-
,1].
∴方程ax2+bx+c=0的两个实数根是-2和1;
由根与系数的关系得,
|
∴c<0,且c=-2a,b=a;
∴不等式cx2+bx+a≥0可化为2x2-x-1≤0,
解得-
| 1 |
| 2 |
∴该不等式的解集为[-
| 1 |
| 2 |
故答案为:[-
| 1 |
| 2 |
点评:本题考查了函数的图象与性质的应用问题,也考查了不等式的解法与应用问题,是综合题.

练习册系列答案
相关题目
执行如图所示的程序框图,则输出的结果为( )


| A、4 | B、9 | C、7 | D、5 |
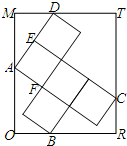 如图矩形ORTM内放置5个大小相同的正方形,其中A、B、C、D都在矩形的边上,若向量
如图矩形ORTM内放置5个大小相同的正方形,其中A、B、C、D都在矩形的边上,若向量