题目内容
已知动圆与x轴相切，且被直线x+y=0截得的弦长为2，求动圆圆心M的轨迹方程．
考点：轨迹方程
专题：计算题,圆锥曲线的定义、性质与方程
分析：利用图象找出等量关系，然后在由半径，弦的一半，弦心距三者组成的直角三角形中建立方程，即可得动圆圆心的轨迹方程．
解答：
解：由题意，设圆心坐标为（x，y），则圆的半径为|y|，弦心距为d=
，
因为弦长为2，故有y2=1+（
）2，整理得x2-y2+2xy+2=0．
| |x+y| | ||
|
因为弦长为2，故有y2=1+（
| |x+y| | ||
|
点评：考查点到直线的距离公式与圆中常用的直角三角形，在圆中由半径，弦心距，弦长的一半组成的直角三角形是直线与圆的位置关系中求九题常用的等量关系．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
已知三条直线m、n、l，三个平面α、β、γ，下列四个命题中，正确的是（ ）
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
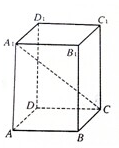如图所示，四棱柱ABCD-A1B1C1D1中，底面ABCD为正方形，高A1A=3，体积为24，则对角线A1C为
函数f（x）=Asin（ωx+φ）（其中A＞0，|φ|＜