题目内容
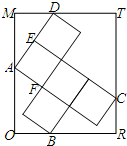如图矩形ORTM内放置5个大小相同的正方形，其中A、B、C、D都在矩形的边上，若向量| BD |
| AE |
| AF |
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：根据题意，根据向量加法的三角形法则，表示出向
=x
-y
，得到x，y的值，进而根据三角形函数的定义，可得角α的三角函数值．
| BD |
| AE |
| AF |
解答：
解：∵
=2
+3
，
即
=3
-2
．
∴x=3，y=3，
∴r=
=13，
∴sinα=
=
，cosα=
=
，tanα=
=
| BD |
| FA |
| AE |
即
| BD |
| AE |
| AF |
∴x=3，y=3，
∴r=
| 32+22 |
∴sinα=
| y |
| r |
2
| ||
| 13 |
| x |
| r |
3
| ||
| 13 |
| y |
| x |
| 2 |
| 3 |
点评：本题考查平面向量基本道理和数量积的运算，三角函数的定义，以及建立坐标系，参数方程解决几何问题，还考查了几何概型，属于较难的题目，应该灵活掌握．
练习册系列答案
相关题目
椭圆C：
+
=1的左、右顶点分别为M、N，点P在C上，且直线PN的斜率为-
，则直线PM斜率为（ ）
| x2 |
| 4 |
| y2 |
| 3 |
| 1 |
| 4 |
A、
| ||
| B、3 | ||
C、-
| ||
| D、-3 |
已知三条直线m、n、l，三个平面α、β、γ，下列四个命题中，正确的是（ ）
A、
| |||||
B、
| |||||
C、
| |||||
D、
|
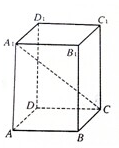如图所示，四棱柱ABCD-A1B1C1D1中，底面ABCD为正方形，高A1A=3，体积为24，则对角线A1C为