Question

【题目】如图，设抛物线的焦点为，是抛物线上一点，过点的切线与轴相交于点，是线段的中点.直线交抛物线于另一点.

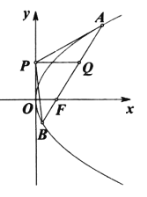
（1）求证：垂直于轴；

（2）求面积的取值范围.

Answer 1

【答案】（1）见解析；（2）

【解析】

（1）由已知，设，只需证明的纵坐标为，设切线的斜率为，写出切线方程，与抛物线联立，令，建立关系，即可证明；

（2）设直线的方程是，与抛物线方程联立，得到坐标关系，将点用表示，结合（1）的结论将三角形面积表示为的函数，根据函数特征求其最值.

（1）设，过的切线方程，

与抛物线方程联立，消去得：

，

令，

即，解得，

故切线的方程是：，

令得，故，又，

故的中点的坐标是，

，所以垂直于轴.

（2）设直线的方程是，

代入抛物线方程得：，设

所以，故，

由（1）题结论可知，

，

设，令，

则，

所以在递减，在递增，

故，

所以面积的取值范围是.