题目内容
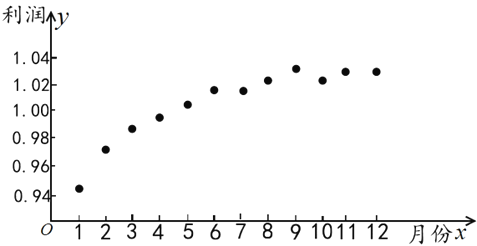
【题目】如图是某创业公司2017年每月份公司利润(单位:百万元)情况的散点图:为了预测该公司2018年的利润情况,根据上图数据,建立了利润y与月份x的两个线性回归模型:①![]() 0.94+0.028
0.94+0.028![]() ;②
;②![]() 0.96+0.032lnx,并得到以下统计值:
0.96+0.032lnx,并得到以下统计值:
模型① | 模型② | |
残差平方和 | 0.000591 | 0.000164 |
总偏差平方和 | 0.006050 | |
(1)请利用相关指数R2判断哪个模型的拟合效果更好;
(2)为了激励员工工作的积极性,公司每月会根据利润的情况进行奖惩,假设本月利润为y1,而上一月利润为y2,计算z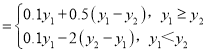 ,并规定:若z≥10,则向全体员工发放奖金总额z元;若z<10,从全体员工每人的工资中倒扣10﹣z元作为惩罚,扣完为止,请根据(1)中拟合效果更好的回归模型,试预测208年4月份该公司的奖惩情况?(结果精确到小数点后两位)
,并规定:若z≥10,则向全体员工发放奖金总额z元;若z<10,从全体员工每人的工资中倒扣10﹣z元作为惩罚,扣完为止,请根据(1)中拟合效果更好的回归模型,试预测208年4月份该公司的奖惩情况?(结果精确到小数点后两位)
参考数据及公式:![]() 1.73,
1.73,![]() 2.24,1n2≈0.69,1n3≈1.10,ln5≈1.61.相关指数R2=1
2.24,1n2≈0.69,1n3≈1.10,ln5≈1.61.相关指数R2=1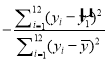 .
.
【答案】(1)模型②![]() 0.96+0.032lnx,的拟合效果更好,详见解析(2)预测2018年4月份公司应该向全体员工发放10.56万元的奖金总额
0.96+0.032lnx,的拟合效果更好,详见解析(2)预测2018年4月份公司应该向全体员工发放10.56万元的奖金总额
【解析】
(1)根据所给数据,分别计算出两种回归方程的相关指数,比较即可.
(2)由(1)知模型②的拟合效果更好,利用模型②预报4月份和3月份的利润y2,y1,代入公式求出z分析即可.
设模型①②的相关指数分别为![]() ,
,![]() ,
,
则![]() 1
1![]() 0.902314,
0.902314,![]() 1
1![]() 0.97289,
0.97289,
所以![]() ,所以模型②
,所以模型②![]() 0.96+0.032lnx,的拟合效果更好.
0.96+0.032lnx,的拟合效果更好.
(2)由(1)知,模型②![]() 0.96+0.032lnx,的拟合效果更好.
0.96+0.032lnx,的拟合效果更好.
则2018年4月份公司的利润的预报值为:y1=0.96+0.032ln16=0.96+0.032×4×ln2≈1.04832(百万元),
2018年3月份公司的利润预报为:y2=0.96+0.32ln15=0.96+0.032(ln3+ln5)≈1.04672(百万元),
所以z=0.1y1+0.5×(y2﹣y1)=0.104832+0.5×0.0016≈0.105632(百万元)≈10.56万元,
因为z≥10,
所以,预测2018年4月份公司应该向全体员工发放10.56万元的奖金总额.

 优学名师名题系列答案
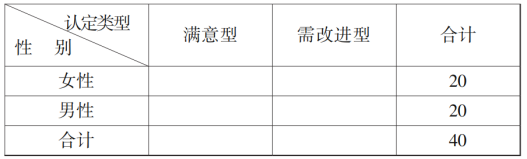
优学名师名题系列答案【题目】某调查机构为了解人们某个产品的使用情况是否与性别有关,在网上进行了问卷调查,在调查结果中随机抽取了50份进行统计,得到如下![]() 列联表:
列联表:
男性 | 女性 | 合计 | |
使用 | 15 | 5 | 20 |
不使用 | 10 | 20 | 30 |
合计 | 25 | 25 | 50 |
(1)请根据调查结果分①析:你有多大把握认为使用该产品与性别有关;
(2)在不使用该产品的人中,按性别用分层抽样抽取6人,再从这6人中随机抽取2人参加某项活动,求这2人中恰有一位女性的概率.
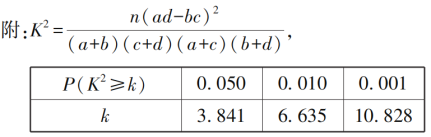
附: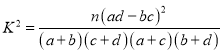
| 0.010 | 0.005 | 0.001 |
| 6.635 | 7.879 | 10.828 |