题目内容
【题目】已知圆![]() ,直线
,直线![]() .
.
(1)若直线![]() 与圆
与圆![]() 交于不同的两点
交于不同的两点![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
(2)若![]() 是直线
是直线![]() 上的动点,过
上的动点,过![]() 作圆
作圆![]() 的两条切线
的两条切线![]() ,切点为
,切点为![]() ,探究:直线
,探究:直线![]() 是否过定点;
是否过定点;
(3)若![]() 为圆
为圆![]() 的两条相互垂直的弦,垂足为
的两条相互垂直的弦,垂足为![]() ,求四边形
,求四边形![]() 的面积的最大值.
的面积的最大值.
【答案】(1)![]() ;(2)见解析;(3)
;(2)见解析;(3)![]()
【解析】
试题分析:(1)依题意圆O的半径![]() =
=![]() ,点O到
,点O到![]() 的距离
的距离![]() ,即
,即![]() =
=![]() ·
·![]() ,所以
,所以![]() ;(2)由题意O、P、C、D四点共圆且在以OP为直径的圆上,设
;(2)由题意O、P、C、D四点共圆且在以OP为直径的圆上,设![]() ,则得
,则得![]() ,即
,即![]() ,而C、D在圆O:
,而C、D在圆O:![]() 上,所以CD方程为
上,所以CD方程为![]() ,整理得
,整理得![]() ,由
,由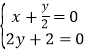 得
得![]() ,故直线CD过定点
,故直线CD过定点![]() ;(3)设圆心到EF、GH的距离分别为
;(3)设圆心到EF、GH的距离分别为![]() ,则
,则![]() , 而
, 而![]() ,
,![]() ,
,![]() ,
,
故![]() , 当且仅当
, 当且仅当![]() 即
即![]() 时,取“=”.
时,取“=”.
试题解析:(1)![]() 点O到
点O到![]() 的距离
的距离![]() 2(分)
2(分)
∴![]() =
=![]() ·
·![]()
![]()
![]() (4分)
(4分)
(2)由题意可知:O、P、C、D四点共圆且在以OP为直径的圆上,设![]()
其方程为:![]()
即:![]()
又C、D在圆O:![]() 上
上
∴![]() 即
即![]() (7分)
(7分)
由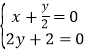 得
得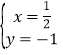
∴直线CD过定点![]() (9分)
(9分)
(3)设圆心O到直线EF、GH的距离分别为![]() .
.
则![]() (11分)
(11分)
∴![]()
![]()
∴![]()
当且仅当![]() 即
即![]() 时,取“=”
时,取“=”
∴四边形EGFH的面积的最大值为![]() (14分)
(14分)

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目