Question

【题目】已知平面内动点P与点A（﹣3，0）和点B（3，0）的连线的斜率之积为﹣ ．
（1）求动点P的轨迹方程；
（2）设点P的轨迹且曲线C，过点（1，0）的直线与曲线C交于M，N两点，记△AMB的面积为S1 ， △ANB的面积为S2 ， 当S1﹣S2取得最大值时，求 的值．

Answer 1

【答案】
（1）

解：由题意可知：2a=6，则a=3，离心率e= = ，

则c=1，b2=a2﹣c2=8，

∴椭圆的标准方程：

（2）

解：设A（x1，y1），B（x2，y2），直线MN的方程：lMN：x=my+1，

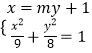，整理得：（8m2+9）y2+16my﹣64=0，

显然△＞0，

则y1+y2=﹣ ，y1y2=﹣ ，

S1= 丨AB丨×丨y1丨=3丨y1丨，同理S2=3丨y2丨，

不妨设，丨y1丨＞丨y2丨，

于是S1﹣S2=3丨y1丨﹣3丨y2丨=3丨y1+y2丨= ，

当S1﹣S2最大时，m≠0，

则S1﹣S2= ≤ =2 ，

当且仅当8丨m丨= ，即m2= ，即m=± ，则S1﹣S2取最大值，

若m= ，则18y2+12 y﹣64=0，

解得：y= ，y1= ，y2= ，

则 =丨 丨=丨 丨= ，

若m=﹣ ，则18y2﹣12 y﹣64=0，

解得：y= ，则y1= ，y2= ，

此时 =丨 丨=丨 丨= ，

综上可知： 的值

【解析】（1）由a=3，利用椭圆的离心率公式，即可求得c，则b2=a2﹣c2=8，即可求得椭圆方程；（2）设直线MN方程，代入椭圆方程，利用韦达定理，S1﹣S2=3丨y1丨﹣3丨y2丨=3丨y1+y2丨利用韦达定理及基本不等式的性质，即可求得面积最大值时，m的取值，分类讨论，分别求得y1及y2 ， 即可求得 的值．