题目内容
【题目】已知函数f(x)=|ax﹣1|
(1)若f(x)≤2的解集为[﹣3,1],求实数a的值;
(2)若a=1,若存在x∈R,使得不等式f(2x+1)﹣f(x﹣1)≤3﹣2m成立,求实数m的取值范围.
【答案】
(1)解:显然a≠0,当a>0时,解集为:[ ![]() ,
, ![]() ],﹣
],﹣ ![]() ,
, ![]() ,无解;
,无解;
当a<0时,解集为:[ ![]() ,﹣
,﹣ ![]() ],令﹣
],令﹣ ![]() =1,
=1, ![]() ,解得a=﹣1,
,解得a=﹣1,
综上a=﹣1.
(2)解:a=1时,令h(x)=f(2x+1)﹣f(x﹣1)=|2x|﹣|x﹣2|= 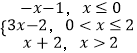 ,
,
由此可知,h(x)在(﹣∞,0],上是单调递减,
在[0,+∞)上单调递增,则x=0时,h(x)取得最小值﹣2,
由题意可知﹣2≤3﹣2m,则实数m的取值范围是(﹣∞, ![]() ].
].
【解析】(1)利用绝对值不等式的解集,列出方程求解即可.(2)利用a=1,若存在x∈R,使得不等式f(2x+1)﹣f(x﹣1)≤3﹣2m成立,化简函数的解析式,通过函数的最小值以及函数的单调性,列出不等式,求解即可.
【考点精析】关于本题考查的绝对值不等式的解法,需要了解含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号才能得出正确答案.

 名校课堂系列答案
名校课堂系列答案【题目】中国共产党第十九次全国代表大会于2017年10月24日在北京召开,会议提出“决胜全面建成小康社会”.某市积极响应开展“脱贫攻坚”,为2020年“全面建成小康社会”贡献力量.为了解该市农村“脱贫攻坚“情况,从某县调查得到农村居民2011年至2017年家庭人均纯收入![]() (单位:百元)的数据如下表:
(单位:百元)的数据如下表:
年份 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
年人均纯收入 | 41 | 45 | 48 | 56 | 60 | 64 | 71 |
注:小康的标准是农村居民家庭年人均纯收入达到8000元.
(1)求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)利用(1)中的回归方程,预测2020年该县农村居民家庭年人均纯收入能否达到“全面建成小康社会”的标准?
附:回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为:
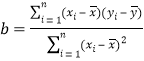 ,
,![]()
【题目】经销商小王对其所经营的某一型号二手汽车的使用年数![]() (0<
(0<![]() ≤10)与销售价格
≤10)与销售价格![]() (单位:万元/辆)进行整理,得到如下的对应数据:
(单位:万元/辆)进行整理,得到如下的对应数据:
使用年数 | 2 | 4 | 6 | 8 | 10 |
售价 | 16 | 13 | 9.5 | 7 | 4.5 |
(Ⅰ)试求![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(附:回归方程![]() 中,
中,
(Ⅱ)已知每辆该型号汽车的收购价格为![]() 万元,根据(Ⅰ)中所求的回归方程,
万元,根据(Ⅰ)中所求的回归方程,
预测![]() 为何值时,小王销售一辆该型号汽车所获得的利润
为何值时,小王销售一辆该型号汽车所获得的利润![]() 最大.
最大.

