ЬтФПФкШн
ЁОЬтФПЁПЙигкКЏЪ§fЃЈxЃЉ![]() ЃЈxЁЪRЃЉЃЌгаЯТЪіЫФИіНсТлЃК
ЃЈxЁЪRЃЉЃЌгаЯТЪіЫФИіНсТлЃК
ЂйШЮвтxЁЪRЃЌЕШЪНfЃЈЉxЃЉ+fЃЈxЃЉЃН0КуГЩСЂЃЛ
ЂкШЮвтx1ЃЌx2ЁЪRЃЌШєx1Ёйx2ЃЌдђвЛЖЈгаfЃЈx1ЃЉЁйfЃЈx2ЃЉЃЛ
ЂлДцдкmЁЪЃЈ0ЃЌ1ЃЉЃЌЪЙЕУЗНГЬ|fЃЈxЃЉ|ЃНmгаСНИіВЛЕШЪЕЪ§ИљЃЛ
ЂмДцдкkЁЪЃЈ1ЃЌ+ЁоЃЉЃЌЪЙЕУКЏЪ§gЃЈxЃЉЃНfЃЈxЃЉЉkxдкRЩЯгаШ§ИіСуЕуЃЎ
ЦфжаАќКЌСЫЫљгае§ШЗНсТлБрКХЕФбЁЯюЮЊЃЈ ЃЉ
A.ЂйЂкЂлЂмB.ЂйЂкЂлC.ЂйЂкЂмD.ЂйЂк
ЁОД№АИЁПB
ЁОНтЮіЁП
ИљОнКЏЪ§ЕФЦцХМадХаЖЯЂйЕФе§ШЗадЃЌИљОнКЏЪ§ЕФЕЅЕїадХаЖЯЂкЕФе§ШЗадЃЌИљОн![]() ЕФЭМЯёХаЖЯЂлЕФе§ШЗадЃЌИљОн
ЕФЭМЯёХаЖЯЂлЕФе§ШЗадЃЌИљОн![]() гы
гы![]() ЕФЭМЯёХаЖЯЂмЕФе§ШЗад.
ЕФЭМЯёХаЖЯЂмЕФе§ШЗад.
КЏЪ§![]() ЕФЖЈвхгђЮЊ
ЕФЖЈвхгђЮЊ![]() ЃЌЧв
ЃЌЧв![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЌМДКЏЪ§ЮЊЦцКЏЪ§ЃЌЙЪЂйе§ШЗ.
ЃЌМДКЏЪ§ЮЊЦцКЏЪ§ЃЌЙЪЂйе§ШЗ.
![]() ЮЊ
ЮЊ![]() ЩЯЕФЦцКЏЪ§ЃЌ
ЩЯЕФЦцКЏЪ§ЃЌ![]() ЃЌЕБ
ЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЮЊдіКЏЪ§ЃЌЫљвд
ЮЊдіКЏЪ§ЃЌЫљвд![]() дк
дк![]() ЩЯЪЧдіКЏЪ§ЃЌЫљвдЂке§ШЗ.
ЩЯЪЧдіКЏЪ§ЃЌЫљвдЂке§ШЗ.
![]() ЪЧ
ЪЧ![]() ЩЯЕФЦцКЏЪ§ЁЂдіКЏЪ§ЃЌЧвЕБ
ЩЯЕФЦцКЏЪ§ЁЂдіКЏЪ§ЃЌЧвЕБ![]() ЪБЃЌ
ЪБЃЌ![]() .дђ
.дђ![]() ЮЊХМКЏЪ§ЃЌЧвЕБ
ЮЊХМКЏЪ§ЃЌЧвЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ![]() ЕндіЃЛЕБ
ЕндіЃЛЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЛЕБ
ЃЛЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЕнМѕ.гЩДЫЛГі
ЕнМѕ.гЩДЫЛГі![]() ЕФЭМЯёШчЯТЭМЫљЪОЃЌгЩЭМПЩжЊЃЌЕБ
ЕФЭМЯёШчЯТЭМЫљЪОЃЌгЩЭМПЩжЊЃЌЕБ![]() ЪЧЃЌ
ЪЧЃЌ![]() гы
гы![]() гаСНИіВЛЭЌЕФНЛЕуЃЌЫљвдЂле§ШЗ.
гаСНИіВЛЭЌЕФНЛЕуЃЌЫљвдЂле§ШЗ.
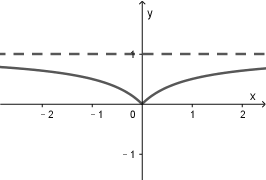
ЛГі![]() гы
гы![]() ЕФЭМЯёШчЯТЭМЫљЪОЃЌгЩЭМПЩжЊЃЌЕБ
ЕФЭМЯёШчЯТЭМЫљЪОЃЌгЩЭМПЩжЊЃЌЕБ![]() ЪБЃЌСНИіКЏЪ§ЭМЯёУЛгаШ§ИіНЛЕуЃЌЫљвдЂме§ШЗ.жЄУїШчЯТЃКЕБ
ЪБЃЌСНИіКЏЪ§ЭМЯёУЛгаШ§ИіНЛЕуЃЌЫљвдЂме§ШЗ.жЄУїШчЯТЃКЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЫљвд
ЃЌЫљвд![]() гк
гк![]() ЕФЭМЯёЯрЧа.ЕБ
ЕФЭМЯёЯрЧа.ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЫљвд
ЃЌЫљвд![]() гк
гк![]() ЕФЭМЯёЯрЧа.НсКЯЭМЯёПЩжЊ
ЕФЭМЯёЯрЧа.НсКЯЭМЯёПЩжЊ![]() гы
гы![]() ЕФЭМЯёжЛгавЛИіЙЋЙВЕуЃЌЕБ
ЕФЭМЯёжЛгавЛИіЙЋЙВЕуЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() гы
гы![]() ЕФЭМЯёвВжЛгавЛИіЙЋЙВЕу.
ЕФЭМЯёвВжЛгавЛИіЙЋЙВЕу.
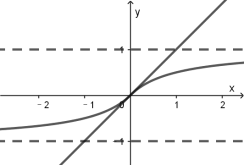
ЙЪбЁЃКB

 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ