题目内容
【题目】如图,多面体![]() 中,底面
中,底面![]() 为菱形,
为菱形,![]() ,
,![]() ,
,![]() ,
,![]() ,且平面
,且平面![]() 底面
底面![]() ,平面
,平面![]() 底面
底面![]() .
.
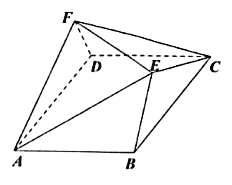
(1)证明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2)![]()
【解析】
(1)要证![]() 平面
平面![]() ,将其转化到
,将其转化到![]() 的平行线上,分别过点
的平行线上,分别过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,连接
,连接![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,下证
,下证![]() ,继而求证结果
,继而求证结果
(2)以![]() 为原点,建立空间直角坐标系
为原点,建立空间直角坐标系![]() ,分别求出平面
,分别求出平面![]() 的法向量和平面
的法向量和平面![]() 的法向量,运用二面角夹角公式求出结果
的法向量,运用二面角夹角公式求出结果
(1)分别过点![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,连接
,连接![]()
因为平面![]() 底面
底面![]() ,平面
,平面![]() 底面
底面![]() ,
,
所以![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,
所以![]() .
.
同理可证,![]() 平面
平面![]() ,所以
,所以![]() .
.
过点![]() 作
作![]() ,垂足为
,垂足为![]()
在![]() 中,
中,![]() ,
,![]() ,则
,则![]()
又![]() ,所以
,所以![]() ,又
,又![]() ,
,
所以四边形![]() 为平行四边形,则
为平行四边形,则![]() .
.
从而![]() ,又
,又![]() ,
,
所以![]() 平面
平面![]() ,故
,故![]() 平面
平面![]() .
.
(2)以![]() 为原点,建立空间直角坐标系
为原点,建立空间直角坐标系![]() 如图所示,
如图所示,
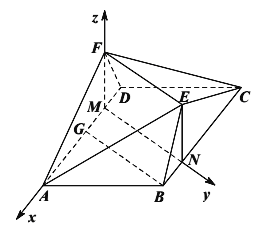
由(1)知![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则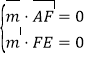 ,即
,即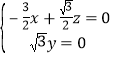 ,
,
解得![]()
令![]() ,则
,则![]() ,
,![]() ,所以
,所以![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则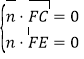 ,即
,即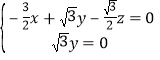 ,
,
解得![]()
令![]() ,则
,则![]() ,
,![]() ,所以
,所以![]() .
.
从而![]() ,故二面角
,故二面角![]() 的余弦值为
的余弦值为![]() .
.

【题目】![]() 年,“非典”爆发,以钟南山为代表的医护工作者经长期努力,抗击了非典.
年,“非典”爆发,以钟南山为代表的医护工作者经长期努力,抗击了非典.![]() 年
年![]() 岁高龄的钟院士再次披挂上阵,逆行武汉抗击新冠疫情。为调查中学生对这一伟大“逆行者”的了解程度,某调查小组随机抽取了某市物化生、政史地的
岁高龄的钟院士再次披挂上阵,逆行武汉抗击新冠疫情。为调查中学生对这一伟大“逆行者”的了解程度,某调查小组随机抽取了某市物化生、政史地的![]() 名高中生,请他们列举钟南山院士在医学上的成就,把能列举钟南山成就不少于
名高中生,请他们列举钟南山院士在医学上的成就,把能列举钟南山成就不少于![]() 项的称为“比较了解”,少于三项的称为“不太了解”他们的调查结果如下:
项的称为“比较了解”,少于三项的称为“不太了解”他们的调查结果如下:
组合 | 0项 | 1项 | 2项 | 3项 | 4项 | 5项 | 5项以上 |
物化生(人) | 1 | 10 | 17 | 14 | 14 | 10 | 4 |
政史地(人) | 0 | 8 | 10 | 6 | 3 | 2 | 1 |
(1)请将下面的2×2列联表补充完整;
组合 | 比较了解 | 不太了解 | 合计 |
物化生 | |||
政史地 | |||
合计 |
(2)判断是否有99%的把握认为,了解钟南山与选择物化生、政史地组合有关?
参考:![]()
![]() .
.
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
【题目】某校高一年级三个班共有学生120名,这三个班的男女生人数如下表所示,已知在全年级中随机抽取1名学生,抽到二班女生的概率是0.2,则![]() _________.现用分层抽样的方法在全年级抽取30名学生,则应在三班抽取的学生人数为________.
_________.现用分层抽样的方法在全年级抽取30名学生,则应在三班抽取的学生人数为________.
一班 | 二班 | 三班 | |
女生人数 | 20 |
|
|
男生人数 | 20 | 20 |
|
【题目】近年来我国电子商务行业迎来发展的新机遇,与此同时,相关管理部门推出了针对电商商品和服务的评价体系.现从评价系统中选出200次成功交易,并对其评价进行统计,对商品好评率为![]() ,对服务好评率为
,对服务好评率为![]() ,其中对商品和服务都做出好评的交易为80次.
,其中对商品和服务都做出好评的交易为80次.
(1)是否可以在犯错误率不超过0.1%的前提下,认为商品好评与服务好评有关?
(2)若针对商品的好评率,采用分层抽样的方式这200次交易中取出5次交易,并从中选择两次交易进行客户回访,求只有一次好评的概率.
注:1.
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
注:2.![]() ,
,![]() .
.