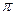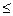题目内容
已知f(x)=sin(2x+
)
(1)求函数f(x)的递减区间;
(2)用五点法作出函数在一个周期内的图象,并说明它是由y=sinx的图象依次经过哪些变换而得到的?
| π |
| 3 |
(1)求函数f(x)的递减区间;
(2)用五点法作出函数在一个周期内的图象,并说明它是由y=sinx的图象依次经过哪些变换而得到的?
(1)对于函数f(x)=sin(2x+
),
令
+2kπ≤2x+
≤
+2kπ(k∈Z),得
+kπ≤x≤
+kπ(k∈Z),
∴函数f(x)的递减区间为[
+kπ,
+kπ],(k∈Z).
(2)列出如下表格:

在直角坐标系中描出点(-
,0),(
,1),(
,0),(
,-1),(
,0).
连成平滑的曲线如图所示,即为函数f(x)=sin(2x+
)在一个周期内的图象,

将y=sinx的图象先向左平移
个单位,再将所得图象上点的纵坐标不变,
横坐标变为原来的一半,可得函数f(x)=sin(2x+
)的图象.
| π |
| 3 |
令
| π |
| 2 |
| π |
| 3 |
| 3π |
| 2 |
| π |
| 12 |
| 7π |
| 12 |
∴函数f(x)的递减区间为[
| π |
| 12 |
| 7π |
| 12 |
(2)列出如下表格:

在直角坐标系中描出点(-
| π |
| 6 |
| π |
| 12 |
| π |
| 3 |
| 7π |
| 12 |
| 5π |
| 6 |
连成平滑的曲线如图所示,即为函数f(x)=sin(2x+
| π |
| 3 |

将y=sinx的图象先向左平移
| π |
| 3 |
横坐标变为原来的一半,可得函数f(x)=sin(2x+
| π |
| 3 |

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目




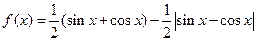 ,则
,则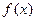 的值域是( )
的值域是( )



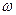 x+
x+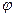 )(
)(