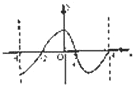
题目内容

y=x-2sinx，x∈[-
π
2
，
π
2
]的图象是（　　）
A．B．
C．D．
当x=0时，y=0-2sin0=0
故函数图象过原点，且f（-x）=-f（x）图象关于原点对称，
可排除B，D．
又∵y'=1-2cosx
∴y′=0⇒cosx=
1
2
⇒x=±
π
3

故函数的单调区间以±
π
3
为分界点，排除答案C．
故只有A满足要求
故选：A．
练习册系列答案
相关题目
（本小题满分12分）
已知函数的最大值为3，的图像的相邻两对称轴间的距离为2，在Y轴上的截距为2.
（Ⅰ）求函数的解析式；（Ⅱ）设数列为其前n项和，求.
已知函数y=f（x）sinx的一部分图象如右图所示，则函数f（x）可以是（　　）
A．2sinxB．2cosxC．-2sinxD．-2cosx
把y=sinx的图象向左平移
π
3
个单位，所得函数图象的解析式为______．
（（10分））已知函数．

（1）求函数的最小正周期和单调递减区间；
设函数f（x）的定义域为[-4，4]，其图象如图，那么不等式
f(x)
sinx
≤0的解集为______．
已知f(x)=sin(2x+
π
3
)
（1）求函数f（x）的递减区间；
（2）用五点法作出函数在一个周期内的图象，并说明它是由y=sinx的图象依次经过哪些变换而得到的？
设ω＞0，若函数f（x）=2sinωx在[-
π
3
，
π
4
，]上单调递增，则ω的取值范围是______．
已知函数y=sin（ωx+φ）（ω＞0，0＜φ＜
π
2
），且此函数的图象如图所示，则点（ω，φ）的坐标是______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网