题目内容

在△ABC中，若b=1，c=
3
，∠C=
2π
3
，则a=（　　）
A．1B．2C．3D．4
由余弦定理得：c2=a2+b2-2abcosC，
又b=1，c=
3
，∠C=
2π
3
，代入得：
3=a2+1-2×（-
1
2
），即a2=1，
由a为△ABC的边，得到a＞0，
解得a=1．
故选A
练习册系列答案
相关题目
两座灯塔A和B与海洋观察站C的距离都等于a Km，灯塔A在观察站C的北偏东20°，灯塔B在观察站C的南偏东40°，则灯塔A与灯塔B的距离为______km．
某渔轮在航行中不幸遇险，发出呼救信号，我海军舰艇在A处获悉后，测得该渔轮在北偏东45°、距离为10海里的C处，并测得渔轮正沿南偏东75°的方向、以每小时9海里的速度向附近的小岛靠拢．我海军舰艇立即以每小时21海里的速度沿直线方向前去营救；则舰艇靠近渔轮所需的时间是多少小时？
△ABC中，a，b，c分别是∠A，∠B，∠C的对边，若a2+b2=2c2，则cosc的最小值为（　　）
A．
3
2
B．
2
2
C．
1
2
D．-
1
2
在△ABC中，a，b，c分别是A，B，C的对边，且满足（sinB+sinA+sinC）（sinB+sinC-sinA）=3sinBsinC．求角A．
在△ABC中，a、b、c分别是角A、B、C的对边，若a=1，c=
3
，B=
5π
6
，则b等于______．
已知△ABC三边满足a2+b2=c2-
3
ab，则此三角形的最大内角为______．
在△ABC中，a，b，c分别为角A，B，C的对边，已知cos2A+6sin2
B+C
2
=4．
（1）求角A的度数；
（2）若a=
3
，b+c=3，求b、c的值．
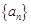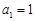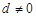已知数列为等差数列，首项，公差，若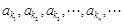成等比数列，且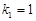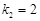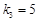，，，则     ．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网