题目内容
16.在正六棱柱ABCDEF-A1B1C1D1E1F1中,用$\overrightarrow{AB}$,$\overrightarrow{AF}$,$\overrightarrow{A{A}_{1}}$表示向量$\overrightarrow{A{D}_{1}}$,其结果为$\overrightarrow{A{D}_{1}}$=$\overrightarrow{A{A}_{1}}$+2($\overrightarrow{AB}$+$\overrightarrow{AF}$).分析 根据六棱柱的几何特征,结合向量加法的三角形法则,可得答案.
解答 解:如下图所示:
在正六棱柱ABCDEF-A1B1C1D1E1F1中,$\overrightarrow{{A}_{1}{D}_{1}}$=$\overrightarrow{AD}$=2($\overrightarrow{AB}$+$\overrightarrow{AF}$),
故$\overrightarrow{A{D}_{1}}$=$\overrightarrow{A{A}_{1}}$+$\overrightarrow{{A}_{1}{D}_{1}}$=$\overrightarrow{A{A}_{1}}$+2($\overrightarrow{AB}$+$\overrightarrow{AF}$),
故答案为:$\overrightarrow{A{A}_{1}}$+2($\overrightarrow{AB}$+$\overrightarrow{AF}$)
点评 本题考查的知识眯是正六棱柱的几何特征,向量加法的三角形法则,难度中档.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目
6.为了了解市民的环保意识,某校高一(1)班50名学生在6月5日(世界环境日)这一天调查了各自家庭丢弃旧塑料袋的情况,有关数据如下表:
(1)求这50户居民每天丢弃旧塑料袋的平均数;
(2)求这50户居民每天丢弃旧塑料袋的方差.
| 每户丢弃旧塑料袋个数 | 2 | 3 | 4 | 5 |
| 户数 | 10 | 10 | 20 | 10 |
(2)求这50户居民每天丢弃旧塑料袋的方差.
1.如图给定的是纸盒的外表面,下列哪一项能由它折叠而成( )


| A. | 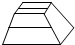 | B. |  | C. |  | D. | 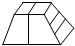 |
8.已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$和圆O:x2+y2=b2,过椭圆上一点P引圆O的两条切线,切点分别为A,B,若椭圆上存在点P,使$\overrightarrow{PA}•\overrightarrow{PB}=0$,则椭圆离心率e的取值范围为( )
| A. | $[\frac{1}{2},1)$ | B. | $[\frac{{\sqrt{2}}}{2},1)$ | C. | $(0,\frac{{\sqrt{2}}}{2}]$ | D. | $[\frac{1}{2},\frac{{\sqrt{2}}}{2}]$ |
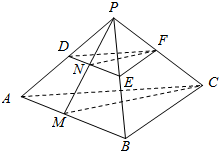 如图,在三棱锥P-ABC中,D,E,F分别是PA,PB,PC的中点.M是AB上一点,连接MC,N是PM与DE的交点,连接NF,求证:NF∥CM.
如图,在三棱锥P-ABC中,D,E,F分别是PA,PB,PC的中点.M是AB上一点,连接MC,N是PM与DE的交点,连接NF,求证:NF∥CM.