题目内容
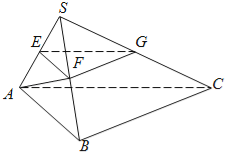
【题目】如图,在三棱锥S-ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB.过A作AF⊥SB,垂足为F,点E,G分别是棱SA,SC的中点.

求证:(1)平面EFG∥平面ABC;
(2)BC⊥SA.
【答案】(1)证明见解析;(2)证明见解析
【解析】试题分析:(1)根据等腰三角形的“三线合一”,证出F为SB的中点.从而得到△SAB和△SAC中,EF∥AB且EG∥AC,利用线面平行的判定定理,证出EF∥平面ABC且EG∥平面ABC.因为EF、EG是平面EFG内的相交直线,所以平面EFG∥平面ABC;
(2)由面面垂直的性质定理证出AF⊥平面SBC,从而得到AF⊥BC.结合AF、AB是平面SAB内的相交直线且AB⊥BC,可得BC⊥平面SAB,从而证出BC⊥SA.
解:(1)∵△ASB中,SA=AB且AF⊥SB,∴F为SB的中点.
∵E、G分别为SA、SC的中点,
∴EF、EG分别是△SAB、△SAC的中位线,可得EF∥AB且EG∥AC.
∵EF平面ABC,AB平面ABC,
∴EF∥平面ABC,同理可得EG∥平面ABC
又∵EF、EG是平面EFG内的相交直线,
∴平面EFG∥平面ABC;
(2)∵平面SAB⊥平面SBC,平面SAB∩平面SBC=SB,
AF平面ASB,AF⊥SB.
∴AF⊥平面SBC.
又∵BC平面SBC,∴AF⊥BC.
∵AB⊥BC,AF∩AB=A,∴BC⊥平面SAB.
又∵SA平面SAB,∴BC⊥SA.

 阅读快车系列答案
阅读快车系列答案【题目】某中学举办安全法规知识竞赛,从参赛的高一、高二学生中各抽出100人的成绩作为样本,对高一年级的100名学生的成绩进行统计,并按![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 分组,得到成绩分布的频率分布直方图(如图)。
分组,得到成绩分布的频率分布直方图(如图)。

(1)若规定60分以上(包括60分)为合格,计算高一年级这次竞赛的合格率;
(2)统计方法中,同一组数据常用该组区间的中点值作为代表,据此,估计高一年级这次知识竞赛的学生的平均成绩;
(3)若高二年级这次竞赛的合格率为![]() ,由以上统计数据填写下面
,由以上统计数据填写下面![]() 列联表,并问是否有
列联表,并问是否有![]() 的把握认为“这次知识竞赛的成绩与年级有关”。
的把握认为“这次知识竞赛的成绩与年级有关”。
高一 | 高二 | 合计 | |
合格人数 | |||
不合格人数 | |||
合计 |
 附:参考数据与公式
附:参考数据与公式
高一 | 合计 | ||
合格人数 | a | b | a+b |
不合格人数 | c | d | c+d |
合计 | a+c | b+d | n |
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |