题目内容
设X为随机变量,X~B 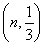 ,若随机变量X的数学期望E(X)=2,则P(X=2)等于( )
,若随机变量X的数学期望E(X)=2,则P(X=2)等于( )
A.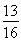 B.
B.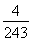 C.
C. D.
D.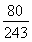
D
【解析】∵E(X)=n×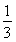 =2,∴n=6.∴P(X=2)=
=2,∴n=6.∴P(X=2)=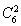
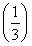 2
2 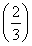 4=
4=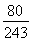

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
设X为随机变量,X~B 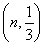 ,若随机变量X的数学期望E(X)=2,则P(X=2)等于( )
,若随机变量X的数学期望E(X)=2,则P(X=2)等于( )
A.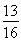 B.
B.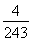 C.
C. D.
D.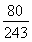
D
【解析】∵E(X)=n×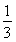 =2,∴n=6.∴P(X=2)=
=2,∴n=6.∴P(X=2)=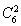
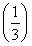 2
2 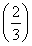 4=
4=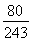

 名校课堂系列答案
名校课堂系列答案