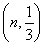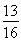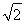题目内容
已知等比数列{an}的所有项均为正数,首项a1=1,且a4,3a3,a5成等差数列.
(1)求数列{an}的通项公式;
(2)数列{an+1-λan}的前n项和为Sn,若Sn=2n-1(n∈N*),求实数λ的值.
(1)an=2n-1(n∈N*).(2)λ=1
【解析】(1)设数列{an}的公比为q,由条件可知q3,3q2,q4成等差数列,∴6q2=q3+q4,∴6=q+q2,
解得q=-3或q=2,∵q>0,∴q=2,
∴数列{an}的通项公式为an=2n-1(n∈N*).
(2)记bn=an+1-λan,则bn=2n-λ·2n-1=(2-λ)2n-1,
若λ=2,则bn=0,Sn=0,不符合条件;
若λ≠2,则 =2,数列{bn}为等比数列,首项为2-λ,公比为2,
=2,数列{bn}为等比数列,首项为2-λ,公比为2,
此时Sn=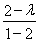 (1-2n)=(2-λ)(2n-1),
(1-2n)=(2-λ)(2n-1),
∵Sn=2n-1(n∈N*),∴λ=1.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目