题目内容
16．
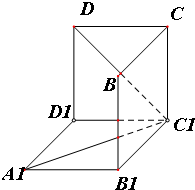如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的．（1）直接写出∠DC1D1在图中的度数和它表示的角的真实度数．
（2）求∠A1C1D的真实度数．
（3）设BC=1m，如果用图示中这样一个装置来盛水，那么最多能盛多少体积的水？
分析 （1）∠DC1D1在图中的度数和它表示的角的真实度数都是45°；
（2）连接DA1，则△A1C1D的三条边都是正方体的面对角线，都是$\sqrt{2}a$，利用等边三角形的性质即可得出；
（3）如果用图示中的装置来盛水，那么最多能盛的水的体积等于三棱锥C1-C B1D1的体积，即可得出．
解答 解：（1）∠DC1D1在图中的度数和它表示的角的真实度数都是45°；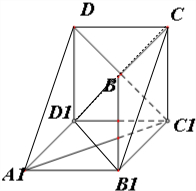
（2）连接DA1，则△A1C1D的三条边都是正方体的面对角线，
都是$\sqrt{2}a$，
∴△A1C1D是等边三角形，
∴∠A1C1D=60°．
（3）如果用图示中的装置来盛水，那么最多能盛的水的体积等于
三棱锥C1-C B1D1的体积，
而${V_{{C_1}-C{B_1}{D_1}}}$=${V_{C-{C_1}{B_1}{D_1}}}$=$\frac{1}{3}{S_{△{B_1}{C_1}{D_1}}}•C{C_1}$=$\frac{1}{6}$．
点评 本题考查了正方体的直观图的性质、等边三角形的性质、三棱锥的体积计算公式，考查了空间想象能力、推理能力与计算能力，属于中档题．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
6．数列1，$\frac{1}{2}$，$\frac{1}{3}$，$\frac{1}{4}$，…的通项公式可能为（ ）
| A． | an=$\frac{1}{n}$ | B． | an=$\frac{1}{n+1}$ | C． | an=n | D． | an=$\frac{1}{2n}$ |
4．某中学高一有21个班、高二有14个班、高三有7个班，现采用分层抽样的方法从这些班中抽取6个班对学生进行视力检查，若从抽取的6个班中再随机抽取2个班做进一步的数据分析，则抽取的2个班均为高一的概率是（ ）
| A． | $\frac{1}{5}$ | B． | $\frac{1}{3}$ | C． | $\frac{3}{5}$ | D． | $\frac{2}{3}$ |
11．与直线4x-3y+5=0关于x轴对称的直线方程为（ ）
| A． | 4x+3y+5=0 | B． | 4x-3y+5=0 | C． | 4x+3y-5=0 | D． | 4x-3y-5=0 |
1．点M（x，y）是不等式组$\left\{\begin{array}{l}{0≤x≤\sqrt{3}}\\{y≤3}\\{x≤\sqrt{3}y}\end{array}\right.$表示的平面区域Ω内的一动点，且不等式2x-y+m≥0恒成立，则的取m值范围是（ ）
| A． | m≥3-2$\sqrt{3}$ | B． | m≥3 | C． | m≥0 | D． | m≥1-2$\sqrt{3}$ |
8．在正方体ABCD-A1B1C1D1中，异面直线BC1与CD1所成角的余弦值为（ ）
| A． | $-\frac{1}{2}$ | B． | $\frac{{\sqrt{2}}}{2}$ | C． | $\frac{{\sqrt{3}}}{2}$ | D． | $\frac{1}{2}$ |