题目内容
5.已知α为锐角,sin2α=$\frac{3}{4}$,则cosα+sinα=$\frac{{\sqrt{7}}}{2}$.分析 由已知可得cosα+sinα>0,由(cosα+sinα)2=1+2sinαcosα=$\frac{7}{4}$,即可得解.
解答 解:∵α为锐角,
∴sinα>0,cosα>0,cosα+sinα>0,
∴(cosα+sinα)2=1+2sinαcosα=1+$\frac{3}{4}$=$\frac{7}{4}$,
∴cosα+sinα=$\frac{{\sqrt{7}}}{2}$.
故答案为:$\frac{{\sqrt{7}}}{2}$.
点评 本题主要考查了二倍角的正弦函数公式的应用,属于基本知识的考查.

练习册系列答案
相关题目
13.平行四边形ABCD的对角线AC与BD相交于O,则( )
| A. | $\overrightarrow{AB}$+$\overrightarrow{AD}$=$\overrightarrow{DB}$ | B. | $\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{BC}$ | C. | $\overrightarrow{AB}$+$\overrightarrow{BO}$=$\overrightarrow{OC}$ | D. | $\overrightarrow{AB}$-$\overrightarrow{BC}$=$\overrightarrow{BD}$ |
20.向量$\vec a$与向量$\vec a-\vec b$的夹角是$\frac{π}{3}$,$|{\vec a}|=1$,$|{\vec a-\vec b}|=3$,则$|{\vec b}|$等于( )
| A. | $\sqrt{6}$ | B. | $\sqrt{7}$ | C. | $2\sqrt{2}$ | D. | 3 |
10.设变量x,y满足约束条件$\left\{\begin{array}{l}x-y+2≤0\\ x+y-8≤0\\ x≥1\end{array}\right.$,则z=2x-y的最大值为( )
| A. | -5 | B. | -1 | C. | 1 | D. | 5 |
14.已知双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0),若a=2b,则双曲线的离心率为( )
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\sqrt{5}$ | C. | $2\sqrt{5}$ | D. | 3 |
11.若命题p:x=4,命题q:x2=16,则p是q的( )
| A. | 必要不充分条件 | B. | 充要条件 | ||
| C. | 充分不必要条件 | D. | 既不充分也不必要条件 |
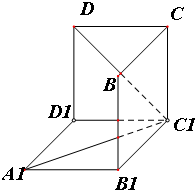 如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的.
如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的. 将数列{an}按如图所示的规律排成一个三角形表,并同时满足以下两个条件:
将数列{an}按如图所示的规律排成一个三角形表,并同时满足以下两个条件: