题目内容
1.点M(x,y)是不等式组$\left\{\begin{array}{l}{0≤x≤\sqrt{3}}\\{y≤3}\\{x≤\sqrt{3}y}\end{array}\right.$表示的平面区域Ω内的一动点,且不等式2x-y+m≥0恒成立,则的取m值范围是( )| A. | m≥3-2$\sqrt{3}$ | B. | m≥3 | C. | m≥0 | D. | m≥1-2$\sqrt{3}$ |
分析 作出不等式组对应的平面区域,利用数形结合将不等式恒成立转化为求最值问题,即可得到结论.
解答 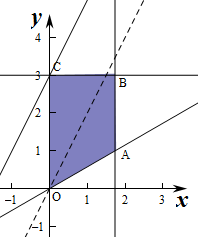 解:若2x-y+m≥0总成立?m≥y-2x总成立即可,
解:若2x-y+m≥0总成立?m≥y-2x总成立即可,
设z=y-2x,即求出z的最大值即可,
作出不等式组对应的平面区域如图:
由z=y-2x得y=2x+z,
平移直线y=2x+z,由图象可知当直线经过点C(0,3)时,直线的截距最大,此时z最大,
此时z=3-0=3,
∴m≥3,
故选:B.
点评 本题主要考查线性规划的应用,将不等式恒成立转换为求目标函数的最值是解决本题的关键.

练习册系列答案
相关题目
11.在△ABC中,内角 A,B,C所对的边分别为a,b,c,若${B}=\frac{π}{3}$,且a,b,c成等比数列,则△ABC一定是( )
| A. | 不等边三角形 | B. | 钝角三角形 | C. | 等腰直角三角形 | D. | 等边三角形 |
6.数列1,2,1,2,…的通项公式不可能为( )
| A. | ${a_n}=\frac{{3+{{(-1)}^n}}}{2}$ | B. | ${a_n}=\frac{{3+{{(-1)}^{n+1}}}}{2}$ | ||
| C. | ${a_n}=\frac{3+cosnπ}{2}$ | D. | ${a_n}=\frac{{3+sin\frac{2n+1}{2}π}}{2}$ |
13.平行四边形ABCD的对角线AC与BD相交于O,则( )
| A. | $\overrightarrow{AB}$+$\overrightarrow{AD}$=$\overrightarrow{DB}$ | B. | $\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{BC}$ | C. | $\overrightarrow{AB}$+$\overrightarrow{BO}$=$\overrightarrow{OC}$ | D. | $\overrightarrow{AB}$-$\overrightarrow{BC}$=$\overrightarrow{BD}$ |
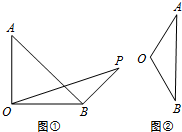 在△AOB中,OA=OB=2,
在△AOB中,OA=OB=2,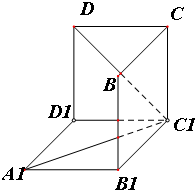 如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的.
如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的.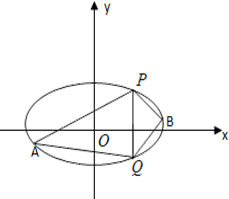 已知椭圆C的中心在原点,焦点在x轴上,离心率等于$\frac{1}{2}$,它的一个顶点恰好是抛物线x2=8$\sqrt{3}$y的焦点.
已知椭圆C的中心在原点,焦点在x轴上,离心率等于$\frac{1}{2}$,它的一个顶点恰好是抛物线x2=8$\sqrt{3}$y的焦点.