题目内容
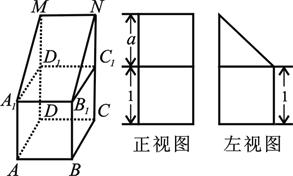
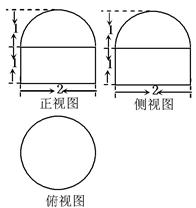
(本小题满分13分)如图,在正方体 的上底面上叠放三棱柱
的上底面上叠放三棱柱
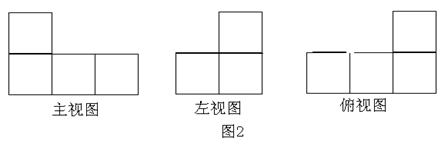
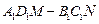 ,该几何体的正视图与左视图如右图所示.
,该几何体的正视图与左视图如右图所示.
(Ⅰ)若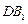
 ,求实数
,求实数 的值;
的值;
(Ⅱ)在(I)的条件下:
① 证明
 平面
平面 ;
;
②求直线 与平面
与平面 所成角的正弦值
所成角的正弦值
 的上底面上叠放三棱柱
的上底面上叠放三棱柱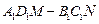 ,该几何体的正视图与左视图如右图所示.
,该几何体的正视图与左视图如右图所示.(Ⅰ)若
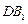
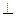
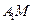 ,求实数
,求实数 的值;
的值;(Ⅱ)在(I)的条件下:
① 证明

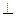 平面
平面 ;
;②求直线
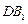 与平面
与平面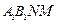 所成角的正弦值
所成角的正弦值

(Ⅰ) =1
=1
(Ⅱ)①见解析
② .
.
 =1
=1(Ⅱ)①见解析
②
 .
.本题主要考查三视图,直线与直线、直线与平面的位置关系等基础知识,考查空间想象能力,推理论证能力,以及运算求解能力,考查化归与转化思想,数形结合思想
解:(Ⅰ)分别以DA、DC、DM为 、y、z轴,建立空间直角坐标系,则D(0,0,0),B1
、y、z轴,建立空间直角坐标系,则D(0,0,0),B1
(1,1,1),A1(1,0,1),C(0,1,0),D1(0,0,1),M(0,0,1+ ),
),
N(0,1,1+ ).
).
 =(1,1,1),
=(1,1,1), =(-1,0,
=(-1,0, ).
).
∵ ⊥
⊥ ,
,
∴ ·
· ="0 "
="0 "  -1+a="0 "
-1+a="0 " 
 ="1." ---------------------4分
="1." ---------------------4分
(Ⅱ)① =(-1,1,-1),
=(-1,1,-1), =(0,
=(0, 1,
1, 1),
1), =(1,0,
=(1,0, 1).
1).
∵ ·
· =0,
=0,  ·
· =0,
=0,
∴ ⊥
⊥ ,
,  ⊥
⊥ ,又ND1
,又ND1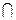 NB1=N.
NB1=N.
∴A1C⊥平面NB1D1. ----------------------------8分
 ②设平面A1B1NM的法向量为
②设平面A1B1NM的法向量为 =(x、y、z),
=(x、y、z),



 ·
· ="0" y=0
="0" y=0
 ·
· ="0 " x-z="0" .
="0 " x-z="0" .
取 =(1,0,1),又
=(1,0,1),又 =(1,1,1),
=(1,1,1),
cos< ·
· >=
>= .
.
设直线DB1与平面A1B1NM所成角为θ,
则sinθ=sin( -<
-< ·
· >)
>)
=cos< ·
· >=
>= .----------------------------13分
.----------------------------13分
解:(Ⅰ)分别以DA、DC、DM为
 、y、z轴,建立空间直角坐标系,则D(0,0,0),B1
、y、z轴,建立空间直角坐标系,则D(0,0,0),B1(1,1,1),A1(1,0,1),C(0,1,0),D1(0,0,1),M(0,0,1+
 ),
),N(0,1,1+
 ).
). =(1,1,1),
=(1,1,1), =(-1,0,
=(-1,0, ).
).∵
 ⊥
⊥ ,
,∴
 ·
· ="0 "
="0 "  -1+a="0 "
-1+a="0 " 
 ="1." ---------------------4分
="1." ---------------------4分(Ⅱ)①
 =(-1,1,-1),
=(-1,1,-1), =(0,
=(0, 1,
1, 1),
1), =(1,0,
=(1,0, 1).
1).∵
 ·
· =0,
=0,  ·
· =0,
=0,∴
 ⊥
⊥ ,
,  ⊥
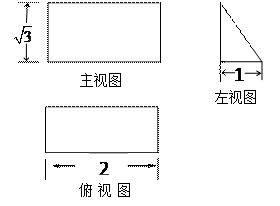
⊥ ,又ND1
,又ND1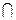 NB1=N.
NB1=N.∴A1C⊥平面NB1D1. ----------------------------8分
 ②设平面A1B1NM的法向量为
②设平面A1B1NM的法向量为 =(x、y、z),
=(x、y、z),


 ·
· ="0" y=0
="0" y=0 ·
· ="0 " x-z="0" .
="0 " x-z="0" . 取
 =(1,0,1),又
=(1,0,1),又 =(1,1,1),
=(1,1,1),cos<
 ·
· >=
>= .
.设直线DB1与平面A1B1NM所成角为θ,
则sinθ=sin(
 -<
-< ·
· >)
>)=cos<
 ·
· >=
>= .----------------------------13分
.----------------------------13分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 直观图和三视图如图所示(主视图、俯视图都是矩形,左视图是直角三角形),设
直观图和三视图如图所示(主视图、俯视图都是矩形,左视图是直角三角形),设 、
、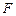 分别为
分别为 和
和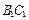 的中点.
的中点. 的体积;
的体积; 平面
平面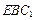 ;
; 平面
平面 .
.




 .
.

 的纬线上,且两地的经度差为
的纬线上,且两地的经度差为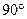 ,若地球的半径为
,若地球的半径为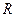 千米,且时速为20千米的轮船从A地到B地最少需要
千米,且时速为20千米的轮船从A地到B地最少需要 小时,则
小时,则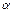 为
为 
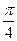
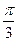
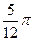
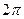
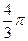
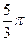
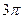
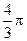 ,则正方体的表面
,则正方体的表面