Question

【题目】已知点， ，点满足，其中， ，且；圆的圆心在轴上，且与点的轨迹相切与点.

（1）求圆的方程；

（2）若点，点是圆上的任意一点，求的取值范围；

（3）过点的两条直线分别与圆交于、两点，若直线、的斜率互为相反数，求证： .

Answer 1

【答案】（1）；（2）；（3）详见解析.

【解析】试题分析：(1)先求出点C的轨迹方程, 依题意,设圆 ,由圆心在轴上,求出 的值,得到圆的方程; (2) 设 ,求出 ,转化为求斜率为 的直线与圆有交点时,纵截距 的范围, 当直线与圆相切时,求出范围; (3)设 ,设直线AP方程为 ,则直线AQ方程为,联立直线与圆方程,求出 的表达式,用 换成 ,求出直线PQ的斜率,与直线AD的斜率相等,所以 .

试题解析：

（1）依题意，可得，所以，所以，所以， ， 三点共线，所以点的轨迹是直线，直线的方程为，整理得.

依题意，可设圆的方程为，整理得，由圆的圆心在轴上，可得，解得.

所以圆的方程为.

（2）设，则， .

令，可化为，它表示斜率为-1的一族平行直线， 是直线在轴上的截距，观察图形，可知当直线与圆相切时， 取得最值， 也取得相应最值.

由，解得， ，所以的取值范围是.

（3）证明：设， .

又设直线的斜率分别为，则直线的斜率为，直线的方程分别为.

由消去可得，则，用代换其中的可得.

所以 .

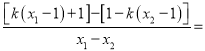
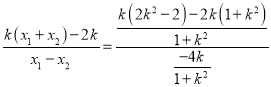
又因为，所以.

点睛: 本题主要考查了直线与圆位置关系, 属于中档题. 解题思路: 在(1)中,由向量关系式得出A,B,C三点共线,求出直线AB的方程,再根据圆D与直线相切,设圆 ,由圆心在轴上,求出 的值,得到圆的方程;在(2)中,注意转化为直线 与圆有交点时,求 的范围; 在(3)中,要证明 ,可以分别求出直线PQ,AD的斜率,看是否相等,得到证明.