题目内容
【题目】已知动圆![]() 过定点
过定点![]() ,且与直线
,且与直线![]() 相切,椭圆
相切,椭圆![]() 的对称轴为坐标轴,
的对称轴为坐标轴,![]() 点为坐标原点,
点为坐标原点,![]() 是其一个焦点,又点
是其一个焦点,又点![]() 在椭圆
在椭圆![]() 上.
上.
(1)求动圆圆心![]() 的轨迹
的轨迹![]() 的标准方程和椭圆
的标准方程和椭圆![]() 的标准方程;
的标准方程;
(2)若过![]() 的动直线
的动直线![]() 交椭圆
交椭圆![]() 于
于![]() 点,交轨迹
点,交轨迹![]() 于
于![]() 两点,设
两点,设![]() 为
为![]() 的面积,
的面积,![]() 为
为![]() 的面积,令
的面积,令![]() 的面积,令
的面积,令![]() ,试求
,试求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() (2)
(2)![]()
【解析】
试题分析:(1)动圆圆心![]() 满足抛物线的定义:
满足抛物线的定义:![]() ,所以方程为
,所以方程为![]() ,而椭圆标准方程的确定,利用待定系数法:
,而椭圆标准方程的确定,利用待定系数法:![]() (2)先表示面积:抛物线中三角形面积,利用焦点,底边OF为常数,高为横坐标之差的绝对值,再根据直线方程与抛物线方程联立,利用韦达定理求解;椭圆中三角形面积,利用A点为定点,底边AF为常数,高为横坐标之差的绝对值,再根据直线方程与椭圆方程联立,利用韦达定理求解;研究
(2)先表示面积:抛物线中三角形面积,利用焦点,底边OF为常数,高为横坐标之差的绝对值,再根据直线方程与抛物线方程联立,利用韦达定理求解;椭圆中三角形面积,利用A点为定点,底边AF为常数,高为横坐标之差的绝对值,再根据直线方程与椭圆方程联立,利用韦达定理求解;研究![]() 函数关系式:是一元函数,可根据直线斜率k取值范围求解
函数关系式:是一元函数,可根据直线斜率k取值范围求解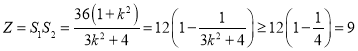
试题解析:(1)依题意,由抛物线的定义易得动点![]() 的轨迹
的轨迹![]() 的标准方程为:
的标准方程为:![]()
依题意可设椭圆![]() 的标准方程为
的标准方程为![]() ,
,
显然有![]() ,∴
,∴![]() ,∴椭圆
,∴椭圆![]() 的标准方程为
的标准方程为![]()
(2)显然直线![]() 的斜率存在,不妨设直线
的斜率存在,不妨设直线![]() 的直线方程为:
的直线方程为:![]() ①
①
联立椭圆![]() 的标准方程
的标准方程![]() ,有
,有![]() ,
,
设![]() 则有
则有![]() ,
,
再将①式联立抛物线方程![]() ,有
,有![]() ,设
,设![]() 得
得![]() ,∴
,∴![]() ,
,
∴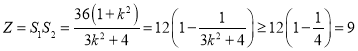 ,
,
∴当![]() 时,
时,![]() ,又
,又![]() ,∴
,∴![]()

练习册系列答案
相关题目