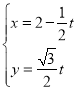题目内容
【题目】已知圆C： 
的圆心为C， 
， 
（Ⅰ）在
中，求
边上的高CD所在的直线方程；
（Ⅱ）求与圆C相切且在两坐标轴上的截距相等的直线方程
【答案】（1）
（2）①
② 
或
或
【解析】试题分析：（1）先求出AB的斜率，然后直线AB与CD垂直，斜率之积为-1得出CD的斜率（2）截距相等要考虑两种情况，当截距都为0时和截距不为0时
当两截距均为0时，设直线方程为
则圆心
到直线的距离为
解出k，
当两截距均不为0时，设直线方程为
则圆心
到直线的距离为
，解出a即可得出方程
试题解析：
解：（Ⅰ）依题意得，圆心为
，半径
， 
，、
直线
的斜率为： 
直线
的方程为： 
，即
（Ⅱ）当两截距均为0时，设直线方程为
则圆心
到直线的距离为
，解得
，得直线为
当两截距均不为0时，设直线方程为
则圆心
到直线的距离为
，解得
，得直线为
或
综上所述，直线方程为
或
或
练习册系列答案
相关题目
