题目内容
20. 空间四边形ABCD中,P、Q、R、H分别是AB、BC、CD、DA的中点.
空间四边形ABCD中,P、Q、R、H分别是AB、BC、CD、DA的中点.(1)求证:四边形PQRH是平行四边形;
(2)若AC=BD,则四边形PQRH是什么四边形?
(3)若AC⊥BD,则四边形PQRH是什么四边形?
(4)空间四边形ABCD满足什么条件时,PQRH是正方形?
分析 (1)只需证明QR∥PH,且QR=PH即可.依据是平行公理四:和同一条直线平行的直线平行.
(2)作出如图的空间四边形,连接AC,BD可得一个三棱锥,将四个中点连接,得到一个四边形,可证明其是一个菱形.
(3)结合图形,由三角形的中位线定理可得PQ∥AC,RH∥AC且PQ=$\frac{1}{2}$AC,RH=$\frac{1}{2}$AC,由平行四边形的定义可得四边形PQRH是平行四边形,再由邻边垂直得到四边形PQRH是矩形.
(4)根据三角形的中位线平行于第三边并等于第三边的一半,先判断出AC=BD,又正方形的四个角都是直角,可以得到正方形的邻边互相垂直,然后证出AC与BD垂直,即可得到四边形ABCD满足的条件.
解答 证明:(1)如图,连接BD.
因为QR是△CBD的中位线,
所以QR∥BD,QR=$\frac{1}{2}$BD.
又因为PH是△ABD的中位线,
所以PH∥BD,PH=$\frac{1}{2}$BD.
根据公理4,QR∥PH,且QR=PH.
所以四边形QRPH是平行四边形.
(2)作出如图的空间四边形,
连接AC,BD可得一个三棱锥,
将四个中点连接,得到一个四边形PQRH,
由中位线的性质知,
PH∥QR,PQ∥RH,
故四边形PQRH是平行四边形,
又AC=BD,
故有PQ=$\frac{1}{2}$AC=$\frac{1}{2}$BD=QR,
故四边形PQRH是菱形.
(3)如图三所示:∵PQ∥AC,RH∥AC且PQ=$\frac{1}{2}$AC,RH=$\frac{1}{2}$AC
∴四边形PQRH是平行四边形
又∵AC⊥BD,
∴PQ⊥QR,
∴四边形PQRH是矩形.
(4)四边形ABCD满足AC=BD,AC⊥BD时,四边形EFGH为正方形.
理由如下:
∵P、Q、R、H分别是四边形ABCD的边AB、BC、CD、AD的中点,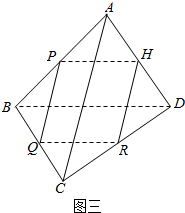
∴PQ∥AC,且PQ=$\frac{1}{2}$AC,
PH∥BD,且PH=$\frac{1}{2}$BD,
∵四边形PQRH是正方形,
∴PQ=QR,PQ⊥QR,
∴AC=BD,AC⊥BD,
∴四边形ABCD满足对角线互相垂直且相等时,四边形EFGH是正方形.
即四边形ABCD满足AC=BD,AC⊥BD时,四边形EFGH为正方形.
点评 本题主要考查了以下知识点:简单几何体和公理四,考查空间中直线与干线之间的位置关系,考查了正方形的性质,三角形的中位线定理,涉及到线线平行的证明,线段的中点,中位线定理,构成平面图形,研究平面图形的形状,是常考类型,属中档题.

 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案| A. | $\frac{3}{4}$ | B. | $\frac{4}{5}$ | C. | $\frac{5}{6}$ | D. | 不存在 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
 已知函数f(x)=logax(a>0,a≠1)
已知函数f(x)=logax(a>0,a≠1)