题目内容
9.设地球的半径为R,在北纬45°纬线圈上有两点A、B,A在西经40°经线上,B在东经50°经线上,求A,B两点间纬线圈的劣弧长及A,B两点间球面距离.分析 A、B两地在同一纬度圈上,计算经度差,求出AB弦长,以及球心角,然后求出球面距离.
解答 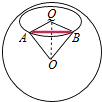 解:地球表面上从A地(北纬45°,西经40°)到B地(北纬45°,东经50°)
解:地球表面上从A地(北纬45°,西经40°)到B地(北纬45°,东经50°)
AB的纬圆半径是$\frac{\sqrt{2}R}{2}$,经度差是90°,
所以A,B两点间纬线圈的劣弧长为$\frac{π}{2}•\frac{\sqrt{2}R}{2}$=$\frac{\sqrt{2}πR}{4}$
又AB=R
所以球心角是θ=$\frac{π}{3}$,
所以A、B两地的球面距离是$\frac{πR}{3}$.
点评 本题考查球面距离及其它计算等基础知识,考查运算求解能力,考查空间想象能力.属于基础题.

练习册系列答案
相关题目
17.急剧增加的人口已经使我们赖以生存的地球不堪重负,控制人口急剧增长的急迫任务摆在我们面前.
(1)世界人口在过去的40 年内翻了一番,问每年人口平均增长率是多少?
(2)我国人口在2003年底达到13.14亿,若将人口平均增长率控制在1%以内,我国人口在2013年底最多有多少亿?
以下对数值可供计算使用:
(1)世界人口在过去的40 年内翻了一番,问每年人口平均增长率是多少?
(2)我国人口在2003年底达到13.14亿,若将人口平均增长率控制在1%以内,我国人口在2013年底最多有多少亿?
以下对数值可供计算使用:
| N | 1.010 | 1.015 | 1.017 | 1.310 | 2.000 |
| lgN | 0.0043 | 0.0065 | 0.0075 | 0.1173 | 0.3010 |
| N | 12.48 | 13.11 | 13.14 | 14.51 | |
| lgN | 1.0962 | 1.1176 | 1.1186 | 1.1616 |
19.直线y=x+2与圆x2+y2=2的位置关系为( )
| A. | 相切 | B. | 相交但直线不过圆心 | ||
| C. | 直线过圆心 | D. | 相离 |
 空间四边形ABCD中,P、Q、R、H分别是AB、BC、CD、DA的中点.
空间四边形ABCD中,P、Q、R、H分别是AB、BC、CD、DA的中点.