题目内容
11．设f（x）=$\left\{\begin{array}{l}{{x}^{2}，x∈[0，1]}\\{2-x，x∈（1，2]}\end{array}\right.$则${∫}_{2}^{0}$f（x）dx=（ ）| A． | $\frac{3}{4}$ | B． | $\frac{4}{5}$ | C． | $\frac{5}{6}$ | D． | 不存在 |
分析 分段函数计算定积分，可分段积分，即：${∫}_{2}^{0}$f（x）dx=${∫}_{0}^{1}x^2dx$+${∫}_{1}^{2}（2-x）dx$．
解答 解：因为f（x）=$\left\{\begin{array}{l}{{x}^{2}，x∈[0，1]}\\{2-x，x∈（1，2]}\end{array}\right.$，所以，
${∫}_{2}^{0}$f（x）dx=${∫}_{0}^{1}x^2dx$+${∫}_{1}^{2}（2-x）dx$
=$\frac{1}{3}$x3${|}_{0}^{1}$+（2x-$\frac{1}{2}$x2）${|}_{1}^{2}$
=$\frac{1}{3}$+$\frac{1}{2}$
=$\frac{5}{6}$，
故选C．
点评 本题主要考查了定积分的运算，涉及分段函数的定积分可分段计算再相加，属于基础题．
练习册系列答案
鹰派教辅衔接教材河北教育出版社系列答案
初中暑期衔接系列答案
相关题目
6．某商店经营一批进价为每件4元的商品，在市场调查时发现，此商品的销售单价x与日销售量y之间有如下关系：
（1）求相关系数．并以此判断销售单价与日销售量之间具有怎样的线性相关关系？
（2）求x，y之间的线性回归方程；
（3）估计销售单价为多少元时，日利润最大？
（参考数据：$\sum_{i=1}^4{{x_i}{y_i}-4\overline x\overline y}$=-11，$\sum_{i=1}^4{x_i^2-4{{（\overline x）}^2}}$=5，$\sum_{i=1}^4{y_i^2-4{{（\overline y）}^2}}$=26）
用最小二乘法求线性回归方程系数公式：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$，r=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sqrt{\sum_{i=1}^{n}{x}_{i}^{2}-n（\overline{x}）^{2}}\sqrt{\sum_{i=1}^{n}{y}_{i}^{2}-n（\overline{y}）^{2}}}$．
| x | 5 | 6 | 7 | 8 |
| y | 10 | 8 | 7 | 3 |
（2）求x，y之间的线性回归方程；
（3）估计销售单价为多少元时，日利润最大？
（参考数据：$\sum_{i=1}^4{{x_i}{y_i}-4\overline x\overline y}$=-11，$\sum_{i=1}^4{x_i^2-4{{（\overline x）}^2}}$=5，$\sum_{i=1}^4{y_i^2-4{{（\overline y）}^2}}$=26）
用最小二乘法求线性回归方程系数公式：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{x}$，r=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sqrt{\sum_{i=1}^{n}{x}_{i}^{2}-n（\overline{x}）^{2}}\sqrt{\sum_{i=1}^{n}{y}_{i}^{2}-n（\overline{y}）^{2}}}$．
16．有两个质地均匀、大小相同的正四面体玩具，每个玩具的各面上分别写有数字1，2，3，4．把两个玩具各抛掷一次，向下的面的数字之和能被5整除的概率为（ ）
| A． | $\frac{1}{16}$ | B． | $\frac{1}{4}$ | C． | $\frac{3}{8}$ | D． | $\frac{1}{2}$ |
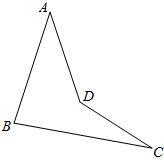空间四边形ABCD中，P、Q、R、H分别是AB、BC、CD、DA的中点．