题目内容
5. 已知函数f(x)=logax(a>0,a≠1)
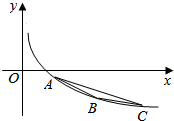
已知函数f(x)=logax(a>0,a≠1)(1)如图,当a=$\frac{1}{2}$时,设A,B,C是函数f(x)=logax的图象上的三点,它们的横坐标分别是t,t+2,t+4(t≥1),记△ABC的面积为S,求S=g(t)的解析式,并求S=g(t)的最大值;
(2)试比较$\frac{1}{2}$f(x)与f($\frac{x+1}{2}$)的大小;
(3)当a=10时,设F(x)=|f(x)|,且满足F(x)=F(t)=2F($\frac{x+t}{2}$)(0<x<t),问是否存在实数t,使得3<t<4.
分析 (1)根据对数函数的图象,将三角形的面积转化为S△ABC=g(t)=S梯形AA1B1B+S梯形BB1C1C-S梯形AA1C1C求解;
(2)分类讨论比较函数值大小;
(3)转为函数H(t)=$t+\frac{1}{t}-2\sqrt{t}$在(3,4)之间是否有零点问题.
解答  解:(1)过A,B,C,分别作AA1,BB1,CC1垂直于x轴,垂足为A1,B1,C1,如右图:
解:(1)过A,B,C,分别作AA1,BB1,CC1垂直于x轴,垂足为A1,B1,C1,如右图:
则S△ABC=g(t)=S梯形AA1B1B+S梯形BB1C1C-S梯形AA1C1C,其中a=$\frac{1}{2}$,所以A,B,C各点纵坐标为负,
=(-$\frac{1}{2}$)[$lo{g}_{\frac{1}{2}}$t+$lo{g}_{\frac{1}{2}}$(t+2)]×2+(-$\frac{1}{2}$)[$lo{g}_{\frac{1}{2}}$(t+2)+loga(t+4)]×2-(-$\frac{1}{2}$)[$lo{g}_{\frac{1}{2}}$t+$lo{g}_{\frac{1}{2}}$(t+4)]×4
=-$lo{g}_{\frac{1}{2}}$$\frac{(t+2)^{2}}{t(t+4)}$=log2(1+$\frac{4}{{t}^{2}+4t}$)(t≥1),
故当t=1时,真数取得最大值,S=g(t)max=g(1)=log2$\frac{9}{5}$,
即g(t)的最大值为log2$\frac{9}{5}$;
(2)∵$\frac{1}{2}$f(x)=f($\sqrt{x}$)且$\frac{x+1}{2}$≥$\sqrt{x}$,∴f($\sqrt{x}$)与f($\frac{x+1}{2}$)的大小关系需要作如下讨论:
①当x=1时,$\sqrt{x}$=$\frac{x+1}{2}$,所以,$\frac{1}{2}$f(x)=f($\frac{x+1}{2}$);
②当x>0且x≠1时,
若0<a<1,则函数y=logax单调递减,所以,f($\sqrt{x}$)>f($\frac{x+1}{2}$),即$\frac{1}{2}$f(x)>f($\frac{x+1}{2}$);
若a>1,则函数y=logax单调递增,所以,f($\sqrt{x}$)<f($\frac{x+1}{2}$),即$\frac{1}{2}$f(x)<f($\frac{x+1}{2}$);
(3)∵a=10,∴F(x)=|f(x)|=|lgx|,而F(x)=F(t)且x<t,
∴x<1<t,且-lgx=lgt,解得xt=1,即x=$\frac{1}{t}$,
又∵$\frac{x+t}{2}$=$\frac{t+\frac{1}{t}}{2}$≥1,所以F($\frac{x+t}{2}$)=lg$\frac{t+\frac{1}{t}}{2}$,
由F(t)=2F($\frac{x+t}{2}$)得lgt=2lg$\frac{t+\frac{1}{t}}{2}$,化简得,$t+\frac{1}{t}-2\sqrt{t}$=0,
记H(t)=$t+\frac{1}{t}-2\sqrt{t}$,由于H(3)=2($\frac{5}{3}$-$\sqrt{3}$)<0,H(4)=$\frac{1}{4}$>0,
所以,函数H(t)在t∈(3,4)内必有零点,
故存在t∈(3,4),使F(x)=F(t)=2F($\frac{x+t}{2}$)成立.
点评 本题主要考查了对数函数的图象与性质,三角形面积的求解,以及函数值大小比较,函数零点的判断,考查了数形结合与分类讨论等解题思想,属于难题.

| A. | $\frac{1}{16}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{8}$ | D. | $\frac{1}{2}$ |
(1)世界人口在过去的40 年内翻了一番,问每年人口平均增长率是多少?
(2)我国人口在2003年底达到13.14亿,若将人口平均增长率控制在1%以内,我国人口在2013年底最多有多少亿?
以下对数值可供计算使用:
| N | 1.010 | 1.015 | 1.017 | 1.310 | 2.000 |
| lgN | 0.0043 | 0.0065 | 0.0075 | 0.1173 | 0.3010 |
| N | 12.48 | 13.11 | 13.14 | 14.51 | |
| lgN | 1.0962 | 1.1176 | 1.1186 | 1.1616 |
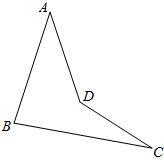 空间四边形ABCD中,P、Q、R、H分别是AB、BC、CD、DA的中点.
空间四边形ABCD中,P、Q、R、H分别是AB、BC、CD、DA的中点.