题目内容
17．已知点P（2，1），Q（-2，-2），过点（0，5）的直线l与线段PQ有公共点，则直线l的斜率k的取值范围是k≤-2或k≥$\frac{7}{2}$．分析 根据题意，画出图形，结合图形，求出直线AP、AQ的斜率，从而求出直线l的斜率k的取值范围．
解答 解：根据题意，画出图形，如图所示：
∵直线AP的斜率是kAP=$\frac{5-1}{0-2}$=-2，
直线BP的斜率是kQA=$\frac{5+2}{0+2}$=$\frac{7}{2}$，
∴直线l的斜率应满足k≤kAP或k≥kAQ，
即k≤-2或k≥$\frac{7}{2}$时，直线l与线段PQ相交；
故答案为：k≤-2或k≥$\frac{7}{2}$．
点评 本题考查了直线方程的应用问题，也考查了数形结合的应用问题，是基础题目．
练习册系列答案
相关题目
8．
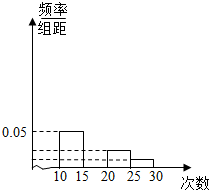对某校高一年级学生参加社区服务次数进行统计，随机抽取M名学生作为样本，得到这M名学生参加社区服务的次数．根据此数据作出了频数与频率的统计表和频率分布直方图：
（1）求出表中M、p、m、n的值；
（2）补全频率分布直方图；若该校高一学生有360人，估计他们参加社区服务的次数在区间[15，20）内的人数；
（3）在所取样本中，从参加社区服务的次数不少于20次的学生中任选2人，求至多一人参加社区服务次数在区间[20，25）内的概率．
对某校高一年级学生参加社区服务次数进行统计，随机抽取M名学生作为样本，得到这M名学生参加社区服务的次数．根据此数据作出了频数与频率的统计表和频率分布直方图：| 分组 | 频数 | 频率 |
| [10，15） | 10 | 0.25 |
| [15，20） | 25 | n |
| [20，25） | m | p |
| [25，30） | 2 | 0.05 |
| 合计 | M | 1 |
（2）补全频率分布直方图；若该校高一学生有360人，估计他们参加社区服务的次数在区间[15，20）内的人数；
（3）在所取样本中，从参加社区服务的次数不少于20次的学生中任选2人，求至多一人参加社区服务次数在区间[20，25）内的概率．
5．已知函数f（x）=2-x和函数$g（x）={log_{\frac{1}{2}}}$x，则函数f（x）与g（x）的图象关于（ ）对称．
| A． | x轴 | B． | y轴 | C． | 直线y=x | D． | 原点 |
12．已知全集I={0，1，2，3}，集合A={1，2}，B={2，3}，则A∪（CIB）=（ ）
| A． | {1} | B． | {2，3} | C． | {0，1，2} | D． | {0，2，3} |