如图.已知l1⊥l2.圆心在l1上.半径为1m的圆O在t=0时与l2相切于点A.圆O沿l1以1m/s的速度匀速向上移动.圆被直线l2所截上方圆弧长记为x.令y=$si{n^2}\frac{x}{2}$.则y与时间t的函数y=fA．B．C．D．题目和参考答案——青夏教育精英家教网—

题目内容

19．

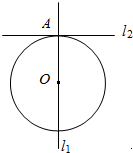如图，已知l₁⊥l₂，圆心在l₁上，半径为1m的圆O在t=0时与l₂相切于点A，圆O沿l₁以1m/s的速度匀速向上移动，圆被直线l₂所截上方圆弧长记为x，令y=$si{n^2}\frac{x}{2}$，则y与时间t（0≤t≤1，单位：s）的函数y=f（t）的图象大致为（　　）

A．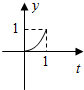

B．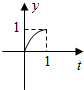

C．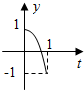

D．

分析通过t=0时y=0，排除选项C、D，利用x的增加的变化率，说明y=sin²x的变化率，得到选项即可．

解答解：因为当t=0时，x=0，对应y=0，所以选项C，D不合题意，
当t由0增加时，x的变化率先快后慢，又y=sin²x在[0，1]上是增函数，所以函数y=f（t）的图象变化先快后慢，
所以选项B满足题意，C正好相反，
故选：B．

点评本题考查函数图象的变换快慢，考查学生理解题意以及视图能力，属于中档题．

练习册系列答案

天利38套高中名校期中期末联考测试卷系列答案

相关题目

5．下列函数中，随x的增大，增长速度最快的是（　　）

y=log₃x

6．（1）计算：0.064${\;}^{-\frac{1}{3}}$+16${\;}^{\frac{3}{4}}$-0.25${\;}^{\frac{1}{2}}$+2log₃6-log₃12；
（2）已知集合A={x|2≤2^x≤16}，B={x|log₃x＞1}，求A∩B，（∁_RB）∪A．

7．函数f（x）=x cos2x在区间[0，2π]上的零点的个数为5．

14．已知p：存在x∈R，mx²+1≤0，q：任意x∈R，x²+mx+1＞0，若p且q为真命题，则实数m的取值范
围是（　　）

4．已知等差数列{a_n}的前n项和为S_n，且a₂=5，S₉=99．
（Ⅰ）求a_n 及S_n；
（Ⅱ）若数列{$\frac{4}{{a}_{n}^{2}-1}$}的前n项和T_n，试求T_n并证明不等式T_n＜1成立．

11．已知全集U=R，集合A={x|x-a≤0}，B={x|x²-3x+2≤0}，且A∪∁_UB=R，则实数a的取值范围是a≥2．

8．

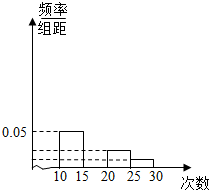对某校高一年级学生参加社区服务次数进行统计，随机抽取M名学生作为样本，得到这M名学生参加社区服务的次数．根据此数据作出了频数与频率的统计表和频率分布直方图：

分组	频数	频率
[10，15）	10	0.25
[15，20）	25	n
[20，25）	m	p
[25，30）	2	0.05
合计	M	1

（1）求出表中M、p、m、n的值；
（2）补全频率分布直方图；若该校高一学生有360人，估计他们参加社区服务的次数在区间[15，20）内的人数；
（3）在所取样本中，从参加社区服务的次数不少于20次的学生中任选2人，求至多一人参加社区服务次数在区间[20，25）内的概率．

9．f（x）为R上奇函数，且x＞0时，f（x）=x²-2^x，则f（-3）=-1．

试题分类