题目内容
16. 已知函数f(x)=x2+2x|x-a|,其中a∈R.
已知函数f(x)=x2+2x|x-a|,其中a∈R.(Ⅰ)当a=-1时,在所给坐标系中作出f(x)的图象;
(Ⅱ)对任意x∈[1,2],函数f(x)的图象恒在函数g(x)=-x+14图象的下方,求实数a的取值范围;
(Ⅲ)若关于x的方程f(x)+1=0在区间(-1,0)内有两个相异根,求实数a的取值范围.
分析 (Ⅰ)依题意当a=-1时,$f(x)={x^2}+2x|{x+1}|=\left\{\begin{array}{l}3{x^2}+2x,x≥-1\\-{x^2}-2x,x<-1\end{array}\right.$,据此可作出图象.
(Ⅱ)由题意,对任意x∈[1,2],只需(f(x)+x)max<14.分类讨论求得(f(x)+x)max ,可得实数a的取值范围.
(Ⅲ)记F(x)=f(x)+1,考虑F(x)在区间(-1,0)内有两个不同的零点即可.分类讨论,求得a的范围.
解答  解:(Ⅰ)依题意当a=-1时,$f(x)={x^2}+2x|{x+1}|=\left\{\begin{array}{l}3{x^2}+2x,x≥-1\\-{x^2}-2x,x<-1\end{array}\right.$,
解:(Ⅰ)依题意当a=-1时,$f(x)={x^2}+2x|{x+1}|=\left\{\begin{array}{l}3{x^2}+2x,x≥-1\\-{x^2}-2x,x<-1\end{array}\right.$,
据此可作出图象如下:
(Ⅱ)由题意,对任意x∈[1,2],f(x)<g(x),即f(x)+x<14恒成立,
只需(f(x)+x)max<14.
另一方面,f(x)=$\left\{\begin{array}{l}{{-x}^{2}+2ax,x<a}\\{{3x}^{2}-2ax,x≥a}\end{array}\right.$,即 f(x)=$\left\{\begin{array}{l}{{-(x-a)}^{2}{+a}^{2},x<a}\\{{3(x-\frac{a}{3})}^{2}-\frac{{a}^{2}}{3},x≥a}\end{array}\right.$.
当a≥0时,f(x)在(-∞,a)和(a,+∞)上均递增,∵f(a)=a2,则f(x)在R上递增,
当a<0时,f(x)在(-∞,a)和$(\frac{a}{3},+∞)$上递增,在$(a,\frac{a}{3})$上递减,
故f(x)在x∈[1,2]上恒单调递增,从而y=f(x)+x在x∈[1,2]上也恒单调递增,
则(f(x)+x)max=f(2)+2=4+4|2-a|+2<14,即|2-a|<2,解得0<a<4,
故实数a的取值范围是(0,4).
(Ⅲ)记F(x)=f(x)+1,考虑F(x)在区间(-1,0)内有两个不同的零点即可.
此时,$F(x)=\left\{{\begin{array}{l}{-{x^2}+2ax+1\begin{array}{l},&{(x≤a)}\end{array}}\\{3{x^2}-2ax+1\begin{array}{l},&{(x>a)}\end{array}}\end{array}}\right.$,即$F(x)=\left\{{\begin{array}{l}{-{{(x-a)}^2}+{a^2}+1\begin{array}{l},&{(x≤a)}\end{array}}\\{3{{(x-\frac{a}{3})}^2}-\frac{a^2}{3}+1\begin{array}{l},&{(x>a)}\end{array}}\end{array}}\right.$,
则由(Ⅱ)可知,
当a≥0时,F(x)=f(x)+1在R上递增,方程f(x)+1=0在区间(-1,0)内至多有一个根,不符合要求,舍去;故a<0.
当x≤a时,令F(x)=0,可得${x_1}=a+\sqrt{{a^2}+1}$(不符合x≤a,舍去)或${x_2}=a-\sqrt{{a^2}+1}$,
但${x_2}=a-\sqrt{{a^2}+1}<-\sqrt{{a^2}+1}<-1$,不在区间(-1,0)内.
当x>a时,F(x)=3x2-2ax+1在区间(-1,0)内必有两个不同的零点,从而(-1,0)⊆(a,+∞),
所以$\left\{\begin{array}{l}-1<\frac{a}{3}<0\\△=4{a^2}-12>0\\ f(0)>0\\ f(-1)>0\\ a≤-1\end{array}\right.$,解得$-2<a<-\sqrt{3}$.
点评 本题主要考查函数的图象,函数与方程的综合应用,体现了转化、分类讨论的数学思想,属于中档题.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案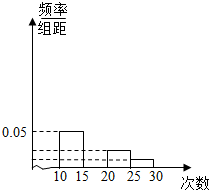 对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图:
对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图:| 分组 | 频数 | 频率 |
| [10,15) | 10 | 0.25 |
| [15,20) | 25 | n |
| [20,25) | m | p |
| [25,30) | 2 | 0.05 |
| 合计 | M | 1 |
(2)补全频率分布直方图;若该校高一学生有360人,估计他们参加社区服务的次数在区间[15,20)内的人数;
(3)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间[20,25)内的概率.
| A. | x轴 | B. | y轴 | C. | 直线y=x | D. | 原点 |