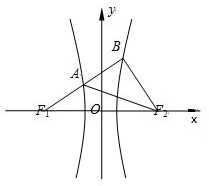
题目内容
双曲线C的中心为原点O,焦点在x轴上,两条渐近线分别为l1,l2,经过右焦点F垂直于l1的直线分别交l1,l2于A,B两点.已知|
|=2|
|,且
与
同向.
(1)求双曲线C的离心率;
(2)设AB被双曲线C所截得的线段的长为4,求双曲线C的方程.
| OA |
| FA |
| BF |
| FA |
(1)求双曲线C的离心率;
(2)设AB被双曲线C所截得的线段的长为4,求双曲线C的方程.
(1)设双曲线方程为
-
=1(a>0,b>0),设渐近线y=
x的倾斜角为α,则∠BOF=∠FOA=α,
由BF⊥OB,可得∠OFA=90°+α,
∵△OFA中,|
|=2|
|,
∴根据正弦定理
=
,得sin∠OFA=2sin∠FOA,
即sin(90°+α)=2sinα,可得cosα=2sinα,
∴tanα=
=
,即
=
,得a=2b,c=
=
b,
因此,双曲线C的离心率e=
=
=
;
(2)由(1)得a=2b,双曲线的方程可化为x2-4y2=4b2…①
设l1的斜率为
=
,可得直线AB的斜率k=-2,得直线AB的方程为y=-2(x-c),
即y=-2(x-
b),…②
将②代入①并化简,得15x2-32
bx+84b2=0
设AB与双曲线的两交点的坐标分别为(x1,y1),(x2,y2),则
x1+x2=
b,x1x2=
…③
∵AB被双曲线所截得的线段长为l=
•|x1-x2|=
∴将③式代入,并可得l=
=
∵根据已知条件得l=4,∴
=4,解得b=3,从而得到a=6.
因此,所求双曲线的方程为
-
=1.
| x2 |
| a2 |
| y2 |
| b2 |
| b |
| a |

由BF⊥OB,可得∠OFA=90°+α,
∵△OFA中,|
| OA |
| FA |
∴根据正弦定理
|
| ||
| sin∠OFA |
|
| ||
| sin∠FOA |
即sin(90°+α)=2sinα,可得cosα=2sinα,
∴tanα=
| sinα |
| cosα |
| 1 |
| 2 |
| b |
| a |
| 1 |
| 2 |
| a2+b2 |
| 5 |
因此,双曲线C的离心率e=
| c |
| a |
| ||
| 2b |
| ||
| 2 |
(2)由(1)得a=2b,双曲线的方程可化为x2-4y2=4b2…①
设l1的斜率为
| b |
| a |
| 1 |
| 2 |
即y=-2(x-
| 5 |
将②代入①并化简,得15x2-32
| 5 |
设AB与双曲线的两交点的坐标分别为(x1,y1),(x2,y2),则
x1+x2=
32
| ||
| 15 |
| 84b2 |
| 15 |
∵AB被双曲线所截得的线段长为l=
| 1+(-2)2 |
| 5[(x1+x2)2-4x1x2] |
∴将③式代入,并可得l=
5[(
|
| 4b |
| 3 |
∵根据已知条件得l=4,∴
| 4b |
| 3 |
因此,所求双曲线的方程为
| x2 |
| 36 |
| y2 |
| 9 |

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目