题目内容

已知双曲线
x2
4
-
y2
9
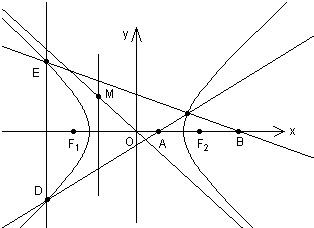
=1，F1，F2是其两个焦点，点M在双曲线上，若∠F1MF2=120°，则△F1MF2的面积为______．
不妨设点M在双曲线的右支上，设|MF1|=m，|MF2|=n．
由双曲线
x2
4
-
y2
9
=1，得a2=4，b2=9，∴c=
a2+b2
=
13
．
则
m-n=2a=4
(2
13
)2=m2+n2-2mncos120°
．
解得mn=12．
∴△F1MF2的面积=
1
2
mnsin120°=3
3
．
故答案为3
3
．
练习册系列答案
相关题目
如图，双曲线
x2
a2
-
y2
b2
=1（a＞0，b＞0）的离心率为
5
2
，F1、F2分别为左、右焦点，M为左准线与渐近线在第二象限内的交点，且
F1M
.
F2M
=-
1
4
．
（I）求双曲线的方程；
（II）设A（m，0）和B(
1
m
，0)（0＜m＜1）是x轴上的两点．过点A作斜率不为0的直线l，使得l交双曲线于C、D两点，作直线BC交双曲线于另一点E．证明直线DE垂直于x轴．中心O为圆心，分别以a和b为半径作大圆和．
已知双曲线的一个焦点与抛物线x2=20y的焦点重合，且其渐近线的方程为3x±4y=0，则该双曲线的标准方程为（　　）
A．
x2
9
-
y2
16
=1		B．
x2
16
-
y2
9
=1		C．
y2
9
-
x2
16
=1		D．
y2
16
-
x2
9
=1
双曲线
y2
9
-
x2
16
=1上的一点P到它一个焦点的距离为4，则点P到另一焦点的距离是（　　）
A．2B．10C．10或2D．14
设双曲线C：
x2
a2
-
y2
b2
=1（a，b＞0）的一条渐近线与抛物线x=y2的一个交点的横坐标为x0，若x0＞
1
2
，则双曲线C的离心率的取值范围是（　　）
A．(1，
6
2
)		B．(1，
3
)		C．(
3
，+∞)		D．(
6
2
，+∞)
若一个椭圆与双曲线x2-
y2
3
=1焦点相同，且过点（-
3
，1）．
（Ⅰ）求这个椭圆的标准方程；
（Ⅱ）求这个椭圆的所有斜率为2的平行弦的中点轨迹方程．
已知双曲线C：
x2
a2
-
y2
b2
=1（a＞0，b＞0）的右焦点为F，过F且斜率为
3
的直线交C于A、B两点，若
AF
=4
FB
，则双曲线C的离心率为______．
双曲线C的中心为原点O，焦点在x轴上，两条渐近线分别为l1，l2，经过右焦点F垂直于l1的直线分别交l1，l2于A，B两点．已知|
OA
|=2|
FA
|，且
BF
与
FA
同向．
（1）求双曲线C的离心率；
（2）设AB被双曲线C所截得的线段的长为4，求双曲线C的方程．
已知双曲线
y2
4
-x2=1，则它的渐近线方程为（　　）
A．y=±2xB．y=±
1
2
x		C．y=±4xD．y=±
1
4
x

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网