Question

在锐角△ABC中，cos B＋cos (A－C)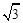＝sin C．

(Ⅰ) 求角A的大小；

(Ⅱ) 当BC＝2时，求△ABC面积的最大值．

 

Answer 1

【答案】

(Ⅰ) A=60°．

(Ⅱ)△ABC面积的最大值为．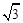 

 

【解析】本题主要考查三角变换、余弦定理、三角形面积公式、均值不等式等基础知识，同时考查三角运算求解能力。

（1）因为cos B＋cos (A－C)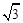＝sin C，

所以－cos (A＋C)＋cos (A－C)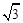＝sin C，得2sin A sin C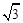＝sinC，故sin A＝

（2）设角A，B，C所对的边分别为a，b，c．由题意知 a＝2，

由余弦定理得  4＝b²＋c²－2bccos60°＝b²＋c²－bc≥bc，

结合三角形面积公式得到结论