题目内容
设不等式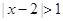 的解集与关于
的解集与关于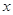 的不等式
的不等式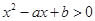 的解集相同.
的解集相同.
(1)求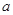 ,
,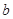 的值;
的值;
(2)求函数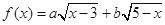 的最大值,以及取得最大值时
的最大值,以及取得最大值时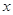 的值.
的值.
(1) 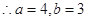 ; (2)
; (2) 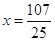 时,
时,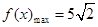
解析试题分析:(1) 通过绝对值的不等式可得解得x的范围,又由二次不等式的解集的含义,可得一个方程组,即可解得相应的结论.
(2)因为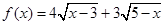 所以利用柯西不等式即可得到函数的最大值,并计算出等号时成立的x的值.本题关键是考查了绝对值不等式的解法,二次不等式的解法,以及柯西不等式的简单变形,对于柯西不等式要关注不等号左右两边的结构.
所以利用柯西不等式即可得到函数的最大值,并计算出等号时成立的x的值.本题关键是考查了绝对值不等式的解法,二次不等式的解法,以及柯西不等式的简单变形,对于柯西不等式要关注不等号左右两边的结构.
试题解析:(1)不等式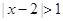 的解集为
的解集为 ,
,
所以,不等式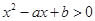 的解集为
的解集为 ,
,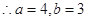 .
.
(2)函数的定义域为 ,显然有
,显然有 ,由柯西不等式可得:
,由柯西不等式可得: 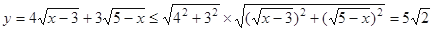 ,
,
当且仅当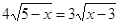 时等号成立,即
时等号成立,即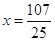 时,函数取得最大值
时,函数取得最大值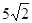 .
.
考点:1.绝对值不等式的解法.2.二次不等式.3.柯西不等式.

练习册系列答案
相关题目
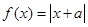 .
.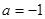 时,求不等式
时,求不等式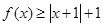 的解集;
的解集;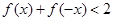 存在实数解,求实数
存在实数解,求实数 的取值范围.
的取值范围. ,其中
,其中 .
. 时,求不等式
时,求不等式 的解集;
的解集;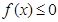 的解集为
的解集为 ,求
,求 的值.
的值.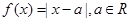
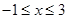 时,
时,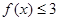 ,求a的取值范围;
,求a的取值范围;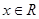 ,
,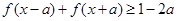 恒成立,求实数a的最小值
恒成立,求实数a的最小值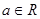 ,解关于
,解关于 的不等式
的不等式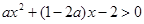 .
.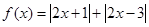 .
. 的不等式
的不等式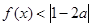 的解集不是空集,求实数
的解集不是空集,求实数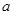 的取值范围;
的取值范围;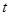 的一元二次方程
的一元二次方程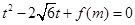 有实根,求实数
有实根,求实数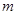 的取值范围.
的取值范围.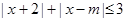 的解集为
的解集为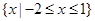 .
. 的值;
的值;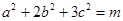 ,求
,求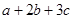 的取值范围.
的取值范围.