题目内容
设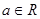 ,解关于
,解关于 的不等式
的不等式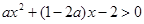 .
.
当 时,不等式的解集为
时,不等式的解集为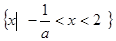 ;
;
当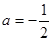 时,不等式的解集为
时,不等式的解集为 ;
;
当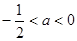 时,不等式的解集为
时,不等式的解集为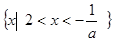 ;
;
当 时,不等式的解集为
时,不等式的解集为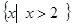 ;
;
当 时,不等式的解集为
时,不等式的解集为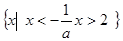
解析试题分析:由实数 的取值是不为零关系到不等的类型,所以要首先考虑
的取值是不为零关系到不等的类型,所以要首先考虑 的情况;、
的情况;、
当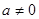 时,要解不等式,需要先解方程
时,要解不等式,需要先解方程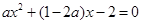 得两根:2和
得两根:2和 ,可以发现实数
,可以发现实数 的取值对两根的大小起决定作用,故又需要依此对的取值进行分类讨论.
的取值对两根的大小起决定作用,故又需要依此对的取值进行分类讨论.
试题解析:解:(1)若 ,则不等式化为
,则不等式化为 ,解得
,解得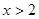 2分
2分
(2)若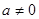 ,则方程的两根分别为2和
,则方程的两根分别为2和 4分
4分
①当 时,解不等式得
时,解不等式得 6分
6分
②当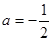 时,不等式的解集为
时,不等式的解集为 8分
8分
③当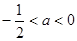 时,解不等式得
时,解不等式得 10分
10分
④当 时,解不等式得
时,解不等式得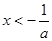 或
或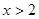 12分
12分
综上所述,当 时,不等式的解集为
时,不等式的解集为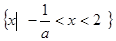 ;
;
当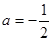 时,不等式的解集为
时,不等式的解集为 ;
;
当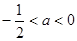 时,不等式的解集为
时,不等式的解集为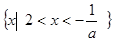 ;
;
当 时,不等式的解集为
时,不等式的解集为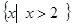 ;
;
当 时,不等式的解集为
时,不等式的解集为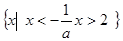 14分
14分
考点:1、一元一次、一元二次不等式的解法;2、分类讨论的思想.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案
相关题目
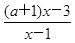 <1.
<1.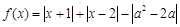 ,若函数
,若函数 的图象恒在
的图象恒在 轴上方,求实数
轴上方,求实数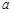 的取值范围.
的取值范围.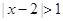 的解集与关于
的解集与关于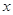 的不等式
的不等式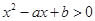 的解集相同.
的解集相同.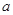 ,
,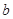 的值;
的值;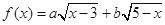 的最大值,以及取得最大值时
的最大值,以及取得最大值时 的不等式
的不等式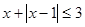 ;
;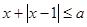 有解,求实数
有解,求实数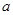 的取值范围.
的取值范围. 若
若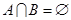 ,求实数
,求实数 的取值范围;
的取值范围;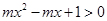 ,对任意实数
,对任意实数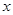 都成立,求
都成立,求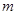 的取值范围.
的取值范围.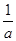 +
+ +
+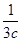 =m,求证:a+2b+3c≥9.
=m,求证:a+2b+3c≥9.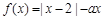 .
.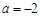 时,解不等式
时,解不等式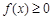 ;
;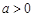 时,不等式
时,不等式 的解集为
的解集为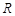 ,求实数
,求实数 的取值范围.
的取值范围.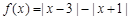 ,
,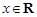 .
. ;
;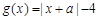 ,且
,且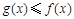 在
在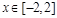 上恒成立,求实数
上恒成立,求实数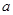 的取值范围.
的取值范围.