题目内容
已知函数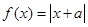 .
.
(1)当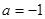 时,求不等式
时,求不等式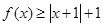 的解集;
的解集;
(2)若不等式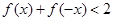 存在实数解,求实数
存在实数解,求实数 的取值范围.
的取值范围.
(1) ;(2)
;(2) .
.
解析试题分析:(1)当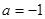 时,不等式
时,不等式 ,化简可得
,化简可得 ,或
,或 ,或
,或 .
.
解出每个不等式组的解集,再取并集,即为所求.
(2)令 ,则由绝对值的意义可得
,则由绝对值的意义可得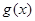 的最小值为
的最小值为 ,依题意可得
,依题意可得 ,由此求得实数
,由此求得实数 的取值范围.
的取值范围.
试题解析:(1)当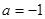 时,不等式
时,不等式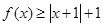 可化为
可化为 ,化简可得
,化简可得 ,或
,或 ,或
,或 .解得
.解得 或
或 ,即所求解集为
,即所求解集为 .
.
(2)令 ,则
,则 ,所以
,所以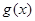 的最小值为
的最小值为 .
.
依题意可得 ,即
,即 .故实数
.故实数 的取值范围是
的取值范围是 .
.
考点:绝对值不等式的解法;函数的零点.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
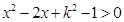 对一切实数x恒成立,则实数k的取值范围是____.
对一切实数x恒成立,则实数k的取值范围是____. (其中
(其中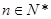 ),区间
),区间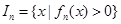 .
. 的长度为
的长度为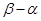 ,求区间
,求区间 的长度;
的长度; ,令
,令 ,
, 的前
的前 项和
项和 ;
; ,
,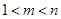 ),使得
),使得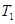 ,
,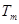 ,
,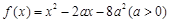 ,记不等式
,记不等式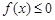 的解集为
的解集为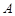 .
.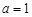 时,求集合
时,求集合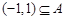 ,求实数
,求实数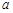 的取值范围.
的取值范围.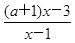 <1.
<1.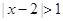 的解集与关于
的解集与关于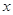 的不等式
的不等式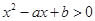 的解集相同.
的解集相同.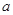 ,
,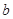 的值;
的值;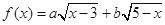 的最大值,以及取得最大值时
的最大值,以及取得最大值时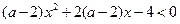 的解集为R,则实数a的取值范围是______________
的解集为R,则实数a的取值范围是______________