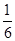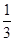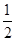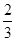题目内容
我校随机抽取100名学生的学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
已知随机抽查这100名学生中的一名学生,抽到积极参加班级工作的学生的概率是0.6,
(1)请将上表补充完整(不用写计算过程)
(2)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关?并说明理由.
(3)从学习积极性高的同学中抽取2人继续调查,设积极参加班级工作的人数为X,求X的分布列和期望.
| 积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
| 学习积极性高 | 40 | ||
| 学习积极性一般 | 30 | ||
| 合计 | 100 |
(1)请将上表补充完整(不用写计算过程)
(2)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关?并说明理由.
(3)从学习积极性高的同学中抽取2人继续调查,设积极参加班级工作的人数为X,求X的分布列和期望.
(1)由题意,
…(3分)
(2)假设学生的学习积极性与对待班级工作的态度无关,由上表
K2=
=
=
=16.667>10.828
故假设不成立,在犯错误概率不超过0.001条件下学生的学习积极性与对待班级工作的态度有关
(此处0.001可以参照其它值)…(7分)
(3)X的所有可能取值为0,1,2
P(X=0)=
,P(X=1)=
,P(X=2)=
E(X)=0×
+1×
+2×
=1.6
| 积极参加班级工作 | 不太主动参加班级工作 | 合计 | |
| 学习积极性高 | 40 | 10 | 50 |
| 学习积极性一般 | 20 | 30 | 50 |
| 合计 | 60 | 40 | 100 |
(2)假设学生的学习积极性与对待班级工作的态度无关,由上表
K2=
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
| 100(40×30-10×20)2 |
| 50×50×60×40 |
| 100×10002 |
| 50×50×60×40 |
故假设不成立,在犯错误概率不超过0.001条件下学生的学习积极性与对待班级工作的态度有关
(此处0.001可以参照其它值)…(7分)
(3)X的所有可能取值为0,1,2
P(X=0)=
| ||
|
| ||||
|
| ||
|
| X | 0 | 1 | 2 | ||||||||||||||||||||
| P |
|
|
|
| ||
|
| ||||
|
| ||
|

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目