题目内容
【题目】动圆P过点
，且与直线
相切，设动圆圆心
的轨迹为曲线
.
（1）求曲线的方程；
（2）过点F的直线交曲线C于A,B两个不同的点，过点A,B分别作曲线C的切线，且二者相交于点M，若直线
的斜率为
，求直线
的方程.
【答案】（1）
（2）
【解析】
（1）设出圆心的坐标，建立方程，计算轨迹，即可。（2）设出直线AB的方程，代入抛物线方程，计算出直线AM和直线BM的方程，相减，得到M点坐标，结合直线
的斜率为
，计算k，得到直线AB的方程。
（1）设点
，则
平方整理得：
（2）由题意可知直线
的斜率一定存在，否则不与曲线
有两个交点
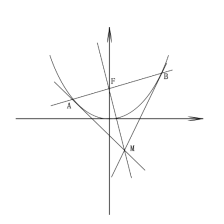
设方程为
，且设点
得
则得
由得：
，所以
∴直线AM的方程为：
①
直线BM的方程为：
②
①－②得：
，
又
，
解得
，
，所以
又
，所以直线的斜率为
，解得
直线的方程为
【题目】近年来，国资委.党委高度重视扶贫开发工作，坚决贯彻落实中央扶贫工作重大决策部署，在各个贫困县全力推进定点扶贫各项工作，取得了积极成效，某贫困县为了响应国家精准扶贫的号召，特地承包了一块土地，已知土地的使用面积以及相应的管理时间的关系如下表所示：
土地使用面积 | 1 | 2 | 3 | 4 | 5 |
管理时间 | 8 | 10 | 13 | 25 | 24 |
并调查了某村300名村民参与管理的意愿，得到的部分数据如下表所示:
愿意参与管理 | 不愿意参与管理 | |
男性村民 | 150 | 50 |
女性村民 | 50 |
（1）求出相关系数
的大小，并判断管理时间
与土地使用面积
是否线性相关？
（2）是否有99.9%的把握认为村民的性别与参与管理的意愿具有相关性？
（3）若以该村的村民的性别与参与管理意愿的情况估计贫困县的情况，则从该贫困县中任取3人，记取到不愿意参与管理的男性村民的人数为,求的分布列及数学期望。
参考公式：
其中
。临界值表：
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
参考数据：
【题目】某工科院校对A、B两个专业的男、女生人数进行调查统计，得到以下表格：
专业A | 专业B | 合计 | |
女生 | 12 | ||
男生 | 46 | 84 | |
合计 | 50 | 100 |
如果认为工科院校中“性别”与“专业”有关，那么犯错误的概率不会超过（ ）
注：
P（x2≥k） | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
A. 0.005B. 0.01C. 0.025D. 0.05
