题目内容
【题目】某种植园在芒果临近成熟时，随机从一些芒果树上摘下100个芒果，其质量分别在
，
，
，
，
，
（单位：克）中，经统计的频率分布直方图如图所示.
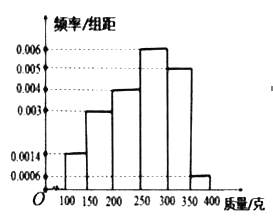
（1）估计这组数据平均数；
（2）现按分层抽样从质量为，的芒果中随机抽取5个，再从这5个中随机抽取2个，求这2个芒果都来自同一个质量区间的概率；
（3）某经销商来收购芒果，以各组数据的中间数代表这组数据的平均值，用样本估计总计，该种植园中还未摘下的芒果大约还有10000个，经销商提出以下两种收购方案：
方案①：所有芒果以9元/千克收购；
方案②：对质量低于250克的芒果以2元/个收购，对质量高于或等于250克的芒果以3元/个收购.
通过计算确定种植园选择哪种方案获利更多.
【答案】（1）255（2）
（3）方案②
【解析】
（1）利用平均数公式求得结果．
（2）抽取的5个芒果中，质量在
和
内的分别有2个和3个．设质量在[250，300）内的3个芒果分别为
，
，
，质量在内的2个芒果分别为
，
．从这5个芒果中选出2个，利用列举法及古典概型公式能求出这2个芒果都来自同一个质量区间的概率．
（3）求出方案①的获利和方案②的获利，从而得到②方案获利更多，应选②方案．
（1）由频率分布直方图知：这组数据的平均数
因此这组数据的平均值大约为255.
（2）利用分层抽样从这两个范围内抽取5个芒果，则质量在内的芒果有2个，记为，，质量在内的芒果有3个，记为，，；
从抽取的5个芒果中抽取2个共有10种不同情况：
，
，
，
，
，
，
，
，
，
.
记事件
为“这2个芒果都来自同一个质量区间”，则有4种不同组合：
，，，，
从而
，
故这2个芒果都来自同一个质量区间的概率为.
（3）方案①收入：
（元）；
方案②：低于250克的芒果收入为：
（元）；
不低于250克的芒果收入为：
（元）；
故方案②的收入为
（元）
由于
，所以选择方案②获利多.
【题目】我市为改善空气环境质量，控制大气污染，政府相应出台了多项改善环境的措施.其中一项是为了减少燃油汽车对大气环境污染.从2018年起大力推广使用新能源汽车，鼓励市民如果需要购车，可优先考虑选用新能源汽车.政府对购买使用新能源汽车进行购物补贴，同时为了地方经济发展，对购买本市企业生产的新能源汽车比购买外地企业生产的新能源汽车补贴高.所以市民对购买使用本市企业生产的新能源汽车的满意度也相应有所提高.有关部门随机抽取本市本年度内购买新能源汽车的
户，其中有
户购买使用本市企业生产的新能源汽车，对购买使用新能源汽车的满意度进行调研，满意度以打分的形式进行.满分分，将分数按照
分成5组，得如下频率分布直方图.
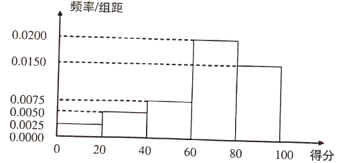
（1）若本次随机抽取的样本数据中购买使用本市企业生产的新能源汽车的用户中有
户满意度得分不少于
分，把得分不少于分为满意.根据提供的条件数据，完成下面的列联表.
满意 | 不满意 | 总计 | |
购本市企业生产的新能源汽车户数 | |||
购外地企业生产的新能源汽车户数 | |||
总计 |
并判断是否有
的把握认为购买使用新能源汽车的满意度与产地有关？
（2）把满意度得分少于
分的用户很不满意用户，在很不满意的用户中有
户购买使用本市企业生产的新能源汽车，其他是购买外地产的.现在从样本中很不满意的用户中随机抽取户进行了解很不满意的具体原因，求这户恰好是一户购买本市企业产的，另一户是购买外地企业产的概率.
