Question

17．已知函数f（x）=e^x，x∈R
（1）若方程f（x）=mx²（m＞0）在（0，+∞）上有两个不同的实根，求m的取值范围；
（2）设a＜b，比较$\frac{f（a）+f（b）}{2}$与$\frac{f（b）-f（a）}{b-a}$的大小，并说明理由．

Answer 1

分析 （1）分离参数m=$\frac{{e}^{x}}{{x}^{2}}$，m＞0，求解导数解不等式得出m′（x）=$\frac{{e}^{x}（x-2）}{{x}^{3}}$=0，x=2，
m′（x）=$\frac{{e}^{x}（x-2）}{{x}^{3}}$＞0，x＞2，m′（x）=$\frac{{e}^{x}（x-2）}{{x}^{3}}$＜0，0＜x＜2，得出单调区间．
（2）作差得出式子$\frac{f（a）+f（b）}{2}$-$\frac{f（b）-f（a）}{b-a}$═$\frac{（b-a）+2+（b-a-2）•{e}^{b-a}}{2（b-a）}$•e^a，
构造函数g（x）=x+2+（x-2）•e^x，判断g′（x）=1+（x-1）•e^x，在（0，+∞）单调递增，
得出g（x）在（0，∞）单调递增，把b-a看作变量x即可得证．

解答 解：函数f（x）=e^x，x∈R
（1）∵方程f（x）=mx²（m＞0），e^x=mx²，x≠0，
∴m=$\frac{{e}^{x}}{{x}^{2}}$，m＞0，
令m（x）=$\frac{{e}^{x}}{{x}^{2}}$，m′（x）=$\frac{{e}^{x}（x-2）}{{x}^{3}}$，x＞0
∵m′（x）=$\frac{{e}^{x}（x-2）}{{x}^{3}}$=0，x=2，
m′（x）=$\frac{{e}^{x}（x-2）}{{x}^{3}}$＞0，x＞2，
m′（x）=$\frac{{e}^{x}（x-2）}{{x}^{3}}$＜0，0＜x＜2
∴m（x）=$\frac{{e}^{x}}{{x}^{2}}$，在（0，2）上单调递减，在（2，+∞）上单调递增，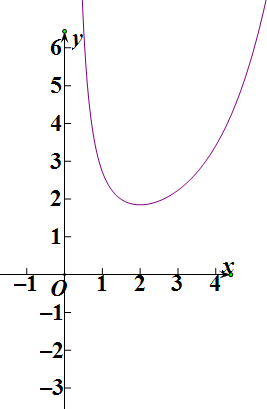

最小值为m（2）=$\frac{{e}^{2}}{4}$，
∵方程f（x）=mx²（m＞0）在（0，+∞）上有两个不同的实根，
∴m（x）=$\frac{{e}^{x}}{{x}^{2}}$，m＞0，与y=m在（0，+∞）上有两个不同交点，
故m$＞\frac{{e}^{2}}{4}$
（2）作差法：$\frac{f（a）+f（b）}{2}$-$\frac{f（b）-f（a）}{b-a}$=$\frac{（b-a+2）f（a）+（b-a）f（b）}{2（b-a）}$=$\frac{（b-a+2）{e}^{a}+（b-a-2）{e}^{b}}{2（b-a）}$
=$\frac{（b-a）+2+（b-a-2）•{e}^{b-a}}{2（b-a）}$•e^a
令g（x）=x+2+（x-2）•e^x，
则g（0）=2-2=0，
∴g′（x）=1+（x-1）•e^x，
而g（0）=0，
∴g′（x）=x•e^x＞0，
∴g′（x）=1+（x-1）•e^x，在（0，+∞）单调递增，
∴g′（x）＞g′（0）=0，
∴g′（x）＞0，
故g（x）在（0，∞）单调递增，
∴g（x）＞g（0）=0，而a＜b，b-a＞0，
∴（b-a）+2+（b-a-2）•e^b-a＞0，

∴$\frac{（b-a+2）{e}^{a}+（b-a-2）{e}^{b}}{2（b-a）}$＞0，

$\frac{（b-a+2）f（a）+（b-a）f（b）}{2（b-a）}$＞0，
$\frac{f（a）+f（b）}{2}$-$\frac{f（b）-f（a）}{b-a}$＞0，
即$\frac{f（a）+f（b）}{2}$＞$\frac{f（b）-f（a）}{b-a}$．

点评 本题考察了运用导数解决问题，构造函数利用多次求解导数，解决，考察了学生多学过的数学思想方法灵活运用的能力，作差比较时常见的方法，但是对于差的处理，运用的方法，学生不一定会．